Difference between revisions of "Fisher's Exact Test"
Jump to navigation
Jump to search
| Line 39: | Line 39: | ||
|- | |- | ||
|SUM || 13 || 12 || 25 | |SUM || 13 || 12 || 25 | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+TABLE | ||
| + | |- | ||
| + | ! COUNT !! PROBABILITY !! PROB | ||
| + | |- | ||
| + | | 0 || 0.0011899313501144164 || 0.0011899313501144164 | ||
| + | |- | ||
| + | | 1 || 0.019038901601830662 || 0.019038901601830662 | ||
| + | |- | ||
| + | | 2 || 0.10471395881006865 || 0.10471395881006865 | ||
| + | |- | ||
| + | | 3 || 0.2617848970251716 || 0.2617848970251716 | ||
| + | |- | ||
| + | | 4 || 0.32723112128146453 || 0 | ||
| + | |- | ||
| + | | 5 || 0.2094279176201373 || 0.2094279176201373 | ||
| + | |- | ||
| + | | 6 || 0.06663615560640732 || 0.06663615560640732 | ||
| + | |- | ||
| + | | 7 || 0.009519450800915331 || 0.009519450800915331 | ||
| + | |- | ||
| + | | 8 || 0.0004576659038901602 || 0.0004576659038901602 | ||
|} | |} | ||
Revision as of 09:19, 27 February 2018
FISHERSEXACTTEST(DataRange,NewTableFlag)
- is the array of x and y values.
- is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
Description
- This function gives the test statistic of the Fisher's Exact Test.
- Since this method is more computationally intense, it is best used for smaller samples.
- Like the chi-square test for (2x2) tables, Fisher's exact test examines the relation between two dimensions of the table (classification into rows vs. columns).
- For experiments with small numbers of participants (below 1,000), Fisher’s is more accurate than the chi-square test or G-test.
- The null hypothesis is that these two classifications are not different.
- The P values in this test are computed by considering all possible tables that could give the row and column totals observed.
Assumptions
- Unlike other statistical tests, there isn’t a formula for Fisher’s.
- To get a result for this test, calculate the probability of getting the observed data using the null hypothesis that the proportions are the same for both sets.
Example
| A | B | |
|---|---|---|
| 1 | 5 | 3 |
| 2 | 8 | 9 |
=FISHERSEXACTTEST([A1:B2],true)
| DATA-0 | DATA-1 | SUM | |
|---|---|---|---|
| 5 | 3 | 8 | |
| 8 | 9 | 17 | |
| SUM | 13 | 12 | 25 |
| COUNT | PROBABILITY | PROB |
|---|---|---|
| 0 | 0.0011899313501144164 | 0.0011899313501144164 |
| 1 | 0.019038901601830662 | 0.019038901601830662 |
| 2 | 0.10471395881006865 | 0.10471395881006865 |
| 3 | 0.2617848970251716 | 0.2617848970251716 |
| 4 | 0.32723112128146453 | 0 |
| 5 | 0.2094279176201373 | 0.2094279176201373 |
| 6 | 0.06663615560640732 | 0.06663615560640732 |
| 7 | 0.009519450800915331 | 0.009519450800915331 |
| 8 | 0.0004576659038901602 | 0.0004576659038901602 |
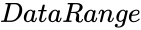 is the array of x and y values.
is the array of x and y values.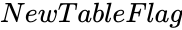 is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.