Difference between revisions of "Manuals/calci/CONFIDENCE"
Jump to navigation
Jump to search
| Line 15: | Line 15: | ||
4. Specify the confidence interval. | 4. Specify the confidence interval. | ||
*Normally once standard error value is calculated, the confidence interval is determined by multiplying the standard error by a constant that reflects the level of significance desired, based on the normal distribution. | *Normally once standard error value is calculated, the confidence interval is determined by multiplying the standard error by a constant that reflects the level of significance desired, based on the normal distribution. | ||
| − | *In <math>CONFIDENCE( | + | *In <math>CONFIDENCE (Alpha,StandardDeviation,Size)</math> , <math>Alpha</math> is the alpha value which is indicating the significance level used to find the value of the confidence level. |
*It equals <math>100*(1-alpha)%</math>, or alpha of 0.05 indicates a 95 percent confidence level. | *It equals <math>100*(1-alpha)%</math>, or alpha of 0.05 indicates a 95 percent confidence level. | ||
*This value is <math> \pm </math> 1.96 | *This value is <math> \pm </math> 1.96 | ||
| Line 30: | Line 30: | ||
*Suppose with the population of 10 for the standard deviation 3.2, with the alpha value 0.2 then, CONFIDENCE(0.2,3.2,10) =1.296839. | *Suppose with the population of 10 for the standard deviation 3.2, with the alpha value 0.2 then, CONFIDENCE(0.2,3.2,10) =1.296839. | ||
*So the Confidence interval value is <math> 10\pm 1.296839= approximately[11.29,8.70]</math>. | *So the Confidence interval value is <math> 10\pm 1.296839= approximately[11.29,8.70]</math>. | ||
| − | |||
==ZOS== | ==ZOS== | ||
Revision as of 14:16, 5 June 2018
CONFIDENCE (Alpha,StandardDeviation,Size)
- is alpha value which is indicating the significance level.
- is the value of the standard deviation.
- is the size of the sample.
Description
- This function gives value of the confidence intervals.
- Confidence intervals are calculated based on the standard error of a measurement.
- It is measures the probability that a population parameter will fall between lower bound and upper bound of the values.
- There are four steps to constructing a confidence interval.
1. Identify a sample statistic. 2. Select a confidence level. 3. Find the margin of error. 4. Specify the confidence interval.
- Normally once standard error value is calculated, the confidence interval is determined by multiplying the standard error by a constant that reflects the level of significance desired, based on the normal distribution.
- In , is the alpha value which is indicating the significance level used to find the value of the confidence level.
- It equals , or alpha of 0.05 indicates a 95 percent confidence level.
- This value is 1.96
- is the standard deviation of the population for the data range.
- is the size of the sample.
- Confidence interval is calculated using the following formula:
.
- So
- where is the sample mean,sigma is the standard deviation.
- This function will give the result as error when
1. Any one of the argument is nonnumeric. 2.Suppose 3. value of s is less than 1.
- Suppose with the population of 10 for the standard deviation 3.2, with the alpha value 0.2 then, CONFIDENCE(0.2,3.2,10) =1.296839.
- So the Confidence interval value is .
ZOS
- The syntax is to calculate CONFIDENCE in ZOS is .
- is value of the significance level.
- is the size of the sample.
- For e.g., CONFIDENCE(0.2,3.1,20)
- CONFIDENCE(0.67,8.3..10.3,51)
Examples
- =CONFIDENCE(0.6,4.6,20) = 0.539393789
- =CONFIDENCE(0.09,8.1,25) = 2.746544290
- =CONFIDENCE(0.001,18.8,50) = 8.74859415
Related Videos
See Also
References
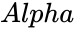 is alpha value which is indicating the significance level.
is alpha value which is indicating the significance level.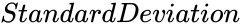 is the value of the standard deviation.
is the value of the standard deviation.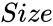 is the size of the sample.
is the size of the sample.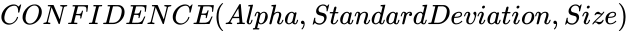 ,
, 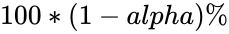 , or alpha of 0.05 indicates a 95 percent confidence level.
, or alpha of 0.05 indicates a 95 percent confidence level.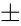 1.96
1.96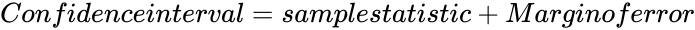 .
.
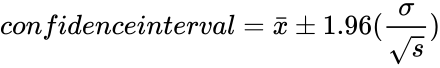
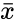 is the sample mean,sigma is the standard deviation.
is the sample mean,sigma is the standard deviation.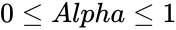 3. value of s is less than 1.
3. value of s is less than 1.
![{\displaystyle 10\pm 1.296839=approximately[11.29,8.70]}](https://wikimedia.org/api/rest_v1/media/math/render/png/08d2b822537efc4fa16cac1a20910b932aae6ee2) .
.