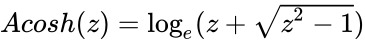Difference between revisions of "Manuals/calci/ACOSH"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*This function gives the Inverse Hyperbolic Cosine of a number. | *This function gives the Inverse Hyperbolic Cosine of a number. | ||
| − | * | + | *Consider 'z' is any positive real number i.e, <math>z \ge 1</math>. |
*Inverse Hyperbolic sine of a number is defined by <math>Acosh(z)=\log_e(z+\sqrt{z^2-1})</math> | *Inverse Hyperbolic sine of a number is defined by <math>Acosh(z)=\log_e(z+\sqrt{z^2-1})</math> | ||
*Also ACOSH(COSH(z))=z | *Also ACOSH(COSH(z))=z | ||
Latest revision as of 17:00, 18 June 2018
ACOSH(Number)
- is any real number.
- ACOSH() returns the inverse hyperbolic cosine of a number.
Description
- This function gives the Inverse Hyperbolic Cosine of a number.
- Consider 'z' is any positive real number i.e, .
- Inverse Hyperbolic sine of a number is defined by
- Also ACOSH(COSH(z))=z
- ACOSH(-2)=NAN , since z<1
Examples
ACOSH(Number)
- Number is any positive real number.
| ACOSH(z) | Value |
| ACOSH(1) | 0 |
| ACOSH(30) | 4.0940666863209 |
| ACOSH(90) | 5.192925985263806 |
Related Videos
See Also
References
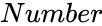 is any real number.
is any real number.
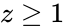 .
.