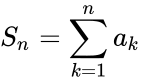Difference between revisions of "Manuals/calci/ARITHMETICSERIES"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
#ARITHMETICSERIES(200,13/7,5) = 200 201.85714285714286 203.71428571428572 205.57142857142858 207.42857142857142 | #ARITHMETICSERIES(200,13/7,5) = 200 201.85714285714286 203.71428571428572 205.57142857142858 207.42857142857142 | ||
#ARITHMETICSERIES(33,-7,8) = 33 26 19 12 5 -2 -9 -16 | #ARITHMETICSERIES(33,-7,8) = 33 26 19 12 5 -2 -9 -16 | ||
| + | #Sn=(a,r,n) => a*(1-r^n) / (1- r); Sn(1,4,5) = 341 | ||
| + | #Sn=(a,r,n) => a*(1-r^n) / (1- r); Sn#; Sn(1,4..10,5) | ||
| + | {| id="TABLE3" class="SpreadSheet blue" | ||
| + | |- class="even" | ||
| + | | class=" " | | ||
| + | |a | ||
| + | |r | ||
| + | |n | ||
| + | |Sn | ||
| + | |||
| + | |- class="odd" | ||
| + | | class=" " | | ||
| + | |1 | ||
| + | |4 | ||
| + | |5 | ||
| + | |341 | ||
| + | |- class="even" | ||
| + | | class=" " | | ||
| + | 1 5 5 781 | ||
| + | 1 6 5 1555 | ||
| + | 1 7 5 2801 | ||
| + | 1 8 5 4681 | ||
| + | 1 9 5 7381 | ||
| + | 1 10 5 11111 | ||
==Related Videos== | ==Related Videos== | ||
Revision as of 01:11, 30 June 2021
ARITHMETICSERIES (Start,Difference,Numbers,OnlyNth)
- is the starting value
- is the difference value of the series.
- is the positive real number.
Description
- This function gives the Arithmetic series of the numbers.
- An arithmetic series is the sum of a sequence {a_k}, k=1, 2, ..., in which each term is computed from the previous one by adding (or subtracting) a constant d.
- Therefore, for k>1,
.
- The sum of the sequence of the first n terms is then given by
Examples
- ARITHMETICSERIES(10,3,6) = 10 13 16 19 22 25
- ARITHMETICSERIES(200,13/7,5) = 200 201.85714285714286 203.71428571428572 205.57142857142858 207.42857142857142
- ARITHMETICSERIES(33,-7,8) = 33 26 19 12 5 -2 -9 -16
- Sn=(a,r,n) => a*(1-r^n) / (1- r); Sn(1,4,5) = 341
- Sn=(a,r,n) => a*(1-r^n) / (1- r); Sn#; Sn(1,4..10,5)
| a | r | n | Sn | |
| 1 | 4 | 5 | 341 | |
|
1 5 5 781 1 6 5 1555 1 7 5 2801 1 8 5 4681 1 9 5 7381 1 10 5 11111 Related VideosSee AlsoReferences
|
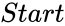 is the starting value
is the starting value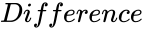 is the difference value of the series.
is the difference value of the series.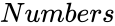 is the positive real number.
is the positive real number. .
.