Difference between revisions of "Manuals/calci/CONFIDENCE"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font size="3"><font face="Times New Roman">'''CONFIDENCE''' ('''alpha''',''' SD''',''' n''')</font></font> <font ...") |
|||
| Line 1: | Line 1: | ||
| + | <div style="font-size:30px">'''CONFIDENCE(a,sd,s)'''</div><br/> | ||
| + | *<math>a</math> is alpha value which is indicating the significance level. | ||
| + | *<math>sd</math> is the standard deviation. | ||
| + | *<math>s</math> is the size of the sample. | ||
| + | |||
| + | |||
| + | ==Description== | ||
| + | *This function gives value of the confidence intervals. | ||
| + | *Confidence intervals are calculated based on the standard error of a measurement. | ||
| + | *It is measures the probability that a population parameter will fall between lower bound and upper bound of the values. | ||
| + | *There are four steps to constructing a confidence interval. | ||
| + | 1. Identify a sample statistic. | ||
| + | 2. Select a confidence level. | ||
| + | 3. Find the margin of error. | ||
| + | 4. Specify the confidence interval. | ||
| + | *Normally once standard error value is calculated, the confidence interval is determined by multiplying the standard error by a constant that reflects the level of significance desired, based on the normal distribution. | ||
| + | *In <math>CONFIDENCE(a,sd,s)</math> , <math>a</math> is the alpha value which is indicating the significance level used to find the value of the confidence level. | ||
| + | *It equals <math>100*(1-alpha)%</math>, or alpha of 0.05 indicates a 95 percent confidence level. | ||
| + | *This value is <math> \plusmn 1.96</math>. | ||
| + | *<math> sd </math> is the standard deviation of the population for the data range. | ||
| + | *<math> s </math> is the size of the sample. | ||
| + | *Confidence interval is calculated using the following formula: | ||
| + | <math>Confidence interval = sample statistic + Margin of error</math>. | ||
| + | *So <math> confidence interval =\bar{x}\plusmn 1.96(\frac{\sigma}{\sqrt {s}})</math> | ||
| + | *where <math>\bar{x}</math> is the sample mean,sigma is the standard deviation. | ||
| + | *This function will give the result as error when | ||
| + | 1. Any one of the argument is nonnumeric. | ||
| + | 2.Suppose <math>0\le alpha\le1 </math> | ||
| + | 3. value of s is less than 1. | ||
| + | *Suppose with the population of 10 for the standard deviation 3.2, with the alpha value 0.2 then, CONFIDENCE(0.2,3.2,10) =1.296839. | ||
| + | *So the Confidence interval value is <math> 10\plusmn 1.296839= approximately[11.29,8.70]</math>. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
<div id="6SpaceContent" class="zcontent" align="left"> | <div id="6SpaceContent" class="zcontent" align="left"> | ||
Revision as of 01:12, 28 March 2014
CONFIDENCE(a,sd,s)
- is alpha value which is indicating the significance level.
- is the standard deviation.
- is the size of the sample.
Description
- This function gives value of the confidence intervals.
- Confidence intervals are calculated based on the standard error of a measurement.
- It is measures the probability that a population parameter will fall between lower bound and upper bound of the values.
- There are four steps to constructing a confidence interval.
1. Identify a sample statistic. 2. Select a confidence level. 3. Find the margin of error. 4. Specify the confidence interval.
- Normally once standard error value is calculated, the confidence interval is determined by multiplying the standard error by a constant that reflects the level of significance desired, based on the normal distribution.
- In , is the alpha value which is indicating the significance level used to find the value of the confidence level.
- It equals , or alpha of 0.05 indicates a 95 percent confidence level.
- This value is .
- is the standard deviation of the population for the data range.
- is the size of the sample.
- Confidence interval is calculated using the following formula:
.
- So
- where is the sample mean,sigma is the standard deviation.
- This function will give the result as error when
1. Any one of the argument is nonnumeric. 2.Suppose 3. value of s is less than 1.
- Suppose with the population of 10 for the standard deviation 3.2, with the alpha value 0.2 then, CONFIDENCE(0.2,3.2,10) =1.296839.
- So the Confidence interval value is .
CONFIDENCE (alpha, SD, n)
Where alpha is the significance level, SD is the population standard deviation for the data range and N is the sample size.
This function returns a value that can be use to construct a confidence interval for a population mean.
· CONFIDENCE returns the error value, when any argument is nonnumeric or alpha is less than or equal to 0 or grater than equal to 1.
· CONFIDENCE returns the error value when SD is less than or equal to 0 or n is less than 1.
CONFIDENCE
Syntax
Remarks
Examples
Description
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 0.05 | 0.993883 | ||
| Row2 | 3 | |||
| Row3 | 35 | |||
| Row4 | ||||
| Row5 | 0 | |||
| Row6 | ||||
| Row7 |
AVEDEV (N1, N2...) Where N1, N 2 ... are positive integers.
Let’s see an example
CONFIDENCE (alpha, SD, n)
i.e. =CONFIDENCE (B2, B3, B4) is 0.9939
 is alpha value which is indicating the significance level.
is alpha value which is indicating the significance level.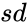 is the standard deviation.
is the standard deviation.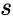 is the size of the sample.
is the size of the sample.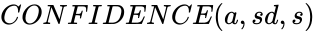 ,
, 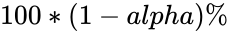 , or alpha of 0.05 indicates a 95 percent confidence level.
, or alpha of 0.05 indicates a 95 percent confidence level.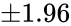 .
.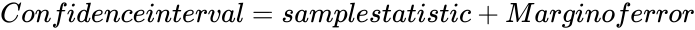 .
.
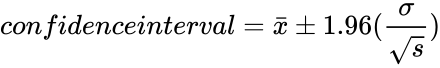
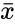 is the sample mean,sigma is the standard deviation.
is the sample mean,sigma is the standard deviation.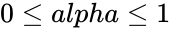 3. value of s is less than 1.
3. value of s is less than 1.
![{\displaystyle 10\pm 1.296839=approximately[11.29,8.70]}](https://wikimedia.org/api/rest_v1/media/math/render/png/08d2b822537efc4fa16cac1a20910b932aae6ee2) .
.