Difference between revisions of "Manuals/calci/FTEST"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''FTEST''' ('''arr1''',''' arr2''') Where '''arr1''' is the first array or range of data and a'''rr2''' is t...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''FTEST(ar1,ar2)'''</div><br/> |
| + | *<math>ar1</math> and <math>ar2 </math> are array of data. | ||
| + | ==Description== | ||
| + | *This function gives the result of F-test. | ||
| + | *The F-test is designed to test if two population variances are equal. | ||
| + | *It does this by comparing the ratio of two variances. | ||
| + | *So, if the variances are equal, the ratio of the variances will be 1.Let X1, ..., Xn and Y1, ..., Ym be independent samples each have a normal distribution . | ||
| + | *It's sample means: X(bar)=1/n summation(i=1 to n)Xi and Y(bar)=1/m summation(i=1 to m)Yi . | ||
| + | *The sample variances : Sx^2=1/n-1 summation(i=1 to n)(Xi-X(bar))^2.and SY^2=1/m-1 summation(i=1 to m)(Yi-Y(bar))^2. | ||
| + | *Then the test statistic= Sx^2/Sy^2 has an F-distribution with n − 1 and m − 1 degrees of freedom. | ||
| + | *In FTEST(ar1,ar2) where ar1 is the data of first array,ar2 is the data of second array. | ||
| + | *The array may be any numbers, names, or refernces that contains numbers. | ||
| + | *Suppose the array contains any text, logical values or empty cells like that values are not considered. | ||
| + | When the ar or ar2 is less than 2 or the variance of the array value is zero then this function will return the result as error. | ||
| + | ==Examples== | ||
| − | + | #Find the correlation coefficients for X and Y values are given below :X={1,2,3,4,5}; Y={11,22,34,43,56} | |
| + | =CORREL(A4:A8,B4:B8)=0.99890610723867 | ||
| + | #The following table gives the math scores and times taken to run 100 m for 10 friends:SCORE(X)={52,25,35,90,76,40}; TIME TAKEN(Y)={11.3,12.9,11.9,10.2,11.1,12.5} | ||
| + | =CORREL(A5:A10,B5:B10)= -0.93626409417769 | ||
| + | #Find the correlation coefficients for X and Y values are given below :X={-4,11,34,87};Y={9,2,59,24} | ||
| + | =CORREL(A1:A4,B1:B4)=0.353184665607273 | ||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/FDIST | FDIST ]] | ||
| + | *[[Manuals/calci/FINV | FINV ]] | ||
| − | |||
| − | |||
| − | |||
| − | + | ==References== | |
| − | + | [http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient| Correlation] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 00:59, 10 December 2013
FTEST(ar1,ar2)
- and are array of data.
Description
- This function gives the result of F-test.
- The F-test is designed to test if two population variances are equal.
- It does this by comparing the ratio of two variances.
- So, if the variances are equal, the ratio of the variances will be 1.Let X1, ..., Xn and Y1, ..., Ym be independent samples each have a normal distribution .
- It's sample means: X(bar)=1/n summation(i=1 to n)Xi and Y(bar)=1/m summation(i=1 to m)Yi .
- The sample variances : Sx^2=1/n-1 summation(i=1 to n)(Xi-X(bar))^2.and SY^2=1/m-1 summation(i=1 to m)(Yi-Y(bar))^2.
- Then the test statistic= Sx^2/Sy^2 has an F-distribution with n − 1 and m − 1 degrees of freedom.
- In FTEST(ar1,ar2) where ar1 is the data of first array,ar2 is the data of second array.
- The array may be any numbers, names, or refernces that contains numbers.
- Suppose the array contains any text, logical values or empty cells like that values are not considered.
When the ar or ar2 is less than 2 or the variance of the array value is zero then this function will return the result as error.
Examples
- Find the correlation coefficients for X and Y values are given below :X={1,2,3,4,5}; Y={11,22,34,43,56}
=CORREL(A4:A8,B4:B8)=0.99890610723867
- The following table gives the math scores and times taken to run 100 m for 10 friends:SCORE(X)={52,25,35,90,76,40}; TIME TAKEN(Y)={11.3,12.9,11.9,10.2,11.1,12.5}
=CORREL(A5:A10,B5:B10)= -0.93626409417769
- Find the correlation coefficients for X and Y values are given below :X={-4,11,34,87};Y={9,2,59,24}
=CORREL(A1:A4,B1:B4)=0.353184665607273
See Also
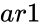 and
and 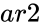 are array of data.
are array of data.