Difference between revisions of "Manuals/calci/IMSUB"
Jump to navigation
Jump to search
(Created page with "<div id="16SpaceContent" align="left"><div class="ZEditBox" align="justify"> Syntax </div></div> ---- <div id="4SpaceContent" align="left"><div class="ZEditBox" align=...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''IMSUB(z1,z2)'''</div><br/> |
| + | *<math>z1 and z2</math> are the complex numbers is of the form <math>a+ib</math> | ||
| + | *<math>n</math> is the power value | ||
| − | + | ==Description== | |
| − | </ | + | *This function gives the difference of the two complex numbers. |
| − | - | + | *IMSUB(z1,z2), Where <math> z1,z2</math> are the complex number is in the form of <math>a+ib</math>. |
| − | < | + | *<math> a </math>& <math>b</math> are the real numbers. <math>i</math> imaginary unit .<math>i=\sqrt{-1}</math>. |
| + | * Let z1=a+ib and z2=c+id. | ||
| + | *The difference of two complex number is:<math>(a+ib)-(c+id)=(a-c)+(b-d)i </math>, where a,b,c and d are real numbers. | ||
| + | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | ||
| − | |||
| − | + | ==Examples== | |
| − | -- | + | #IMSUB("6+4i","5+3i")=1+1i |
| − | + | #IMSUB("3+4i","6+7i")=-3-3i | |
| + | #IMSUB("8","9+10i")=-1-10i | ||
| + | #IMSUB("5+7i","3")=2+7i | ||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/IMREAL | IMREAL ]] | ||
| + | *[[Manuals/calci/IMSUM | IMSUM ]] | ||
| + | *[[Manuals/calci/IMAGINARY | IMAGINARY ]] | ||
| + | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==References== | |
| − | + | [http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 22:41, 18 December 2013
IMSUB(z1,z2)
- are the complex numbers is of the form
- is the power value
Description
- This function gives the difference of the two complex numbers.
- IMSUB(z1,z2), Where are the complex number is in the form of .
- & are the real numbers. imaginary unit ..
- Let z1=a+ib and z2=c+id.
- The difference of two complex number is:, where a,b,c and d are real numbers.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMSUB("6+4i","5+3i")=1+1i
- IMSUB("3+4i","6+7i")=-3-3i
- IMSUB("8","9+10i")=-1-10i
- IMSUB("5+7i","3")=2+7i
See Also
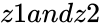 are the complex numbers is of the form
are the complex numbers is of the form 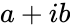
 is the power value
is the power value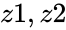 are the complex number is in the form of
are the complex number is in the form of  &
& 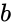 are the real numbers.
are the real numbers.  imaginary unit .
imaginary unit .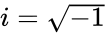 .
.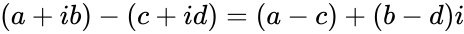 , where a,b,c and d are real numbers.
, where a,b,c and d are real numbers.