Difference between revisions of "Manuals/calci/IMABS"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''IMABS(in)'''</div><br/> | <div style="font-size:30px">'''IMABS(in)'''</div><br/> | ||
| − | * | + | *where <math>iN</math> is the complex number of the form <math>x+iy</math> |
==Description== | ==Description== | ||
| − | *This function gives the absolute value of a complex number of the form x+iy. | + | *This function gives the absolute value of a complex number of the form <math>x+iy</math>. |
| − | *Complex number z=x+iy, where x&y are real numbers and i is the imaginary unit i=sqrt | + | *Complex number <math>z=x+iy</math>, where <math>x</math> & <math>y</math> are real numbers and <math>i</math> is the imaginary unit <math>i=\sqrt{-1}</math>. |
*A complex number's absolute value is measured from zero on the complex number plane. | *A complex number's absolute value is measured from zero on the complex number plane. | ||
| − | *We can use COMPLEX function to convert | + | *We can use COMPLEX function to convert real and imaginary number into a complex number. |
| − | *The absolute value of a complex number is IMABS(z)=|z|=sqrt | + | *The absolute value of a complex number is <math>IMABS(z)=|z|=\sqrt{x^2+y^2}<math> |
==Examples== | ==Examples== | ||
Revision as of 22:45, 19 November 2013
IMABS(in)
- where is the complex number of the form
Description
- This function gives the absolute value of a complex number of the form .
- Complex number , where & are real numbers and is the imaginary unit .
- A complex number's absolute value is measured from zero on the complex number plane.
- We can use COMPLEX function to convert real and imaginary number into a complex number.
- The absolute value of a complex number is <math>IMABS(z)=|z|=\sqrt{x^2+y^2}<math>
Examples
- IMABS("6+8i")=10
- IMABS("5-7i")=SQRT(74)=8.60232
- IMABS("-3-5i")=SQRT(34)=5.83095
See Also
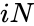 is the complex number of the form
is the complex number of the form 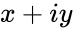
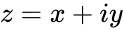 , where
, where  &
& 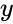 are real numbers and
are real numbers and  is the imaginary unit
is the imaginary unit 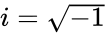 .
.