Difference between revisions of "Manuals/calci/GAMMADIST"
Jump to navigation
Jump to search
| Line 13: | Line 13: | ||
*It is for all complex numbers except the negative integers and zero. | *It is for all complex numbers except the negative integers and zero. | ||
*The Probability Density Function of Gamma function using Shape, rate parameters is: | *The Probability Density Function of Gamma function using Shape, rate parameters is: | ||
| − | <math> f(x; \alpha,\beta)=\frac{x^{\alpha-1} e^- | + | <math> f(x; \alpha,\beta)=\frac{x^{\alpha-1} e^{-\frac {x}{\beta}}}{\beta^{\alpha} Gamma(\alpha)}</math>, for |
| + | :<math>x, \alpha , \beta > 0 </math>, where <math>e</math> is the natural number(e = 2.71828...), <math>\alpha</math> is the number of occurrences of an event, and <math>Gamma(\alpha)</math> is the Gamma function. | ||
*The standard Gamma Probability Density function is: | *The standard Gamma Probability Density function is: | ||
<math>f(x, \alpha)=\frac{x^{\alpha-1} e^{-x}}{Gamma(\alpha)}</math>. | <math>f(x, \alpha)=\frac{x^{\alpha-1} e^{-x}}{Gamma(\alpha)}</math>. | ||
Revision as of 00:04, 4 December 2013
GAMMADIST(x,alpha,beta,cu)
- is the value of the distribution,
- and are the value of the parameters
- is the logical value like true or false.
Description
- This function gives the value of the Gamma Distribution.
- The Gamma Distribution can be used in a queuing models like, the amount of rainfall accumulated in a reservoir. *This distribution is the Continuous Probability Distribution with two parameters Failed to parse (syntax error): {\displaystyle \alpha & \beta} .
- In GAMMADIST(x,alpha,beta,cu), is the value of the distribution, is called shape parameter and is the rate parameter of the distribution and is the logical value like TRUE or FALSE.
- If is TRUE, then this function gives the Cumulative Distribution value and if is FALSE then it gives the Probability Density Function.
- The gamma function is defined by :
.
- It is for all complex numbers except the negative integers and zero.
- The Probability Density Function of Gamma function using Shape, rate parameters is:
, for
- , where is the natural number(e = 2.71828...), is the number of occurrences of an event, and is the Gamma function.
- The standard Gamma Probability Density function is:
.
- The Cumulative Distribution Function of Gamma is Failed to parse (syntax error): {\displaystyle F(x;\alpha,\beta)=[\gamma(\alpha,\frac{x}{\beta}}{Gamma(\alpha)}} , or Failed to parse (syntax error): {\displaystyle F(x;\alpha,\beta)= e^-{\frac {x}{\beta}} \sum_{i=k}^{\infty}\frac{1}{i!}{\frac{x}{ß}}^i} for any positive integer .
- When alpha is a positive integer, then the distribution is called Erlang distribution.
- If the shape parameter α is held fixed, the resulting one-parameter family of distributions is a natural exponential family.
- For a positive integer n, when alpha = n/2, beta = 2, and cu= TRUE, GAMMADIST returns (1 - CHIDIST(x)) with n degrees of freedom.
- This function shows the result as error when 1.Any one of the argument is non numeric
2. x<0, alpha<=0 or beta<=0
 is the value of the distribution,
is the value of the distribution,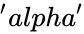 and
and 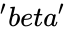 are the value of the parameters
are the value of the parameters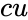 is the logical value like true or false.
is the logical value like true or false.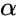 is called shape parameter and
is called shape parameter and  is the rate parameter of the distribution and
is the rate parameter of the distribution and 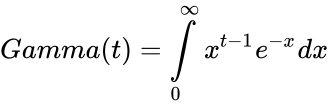 .
.
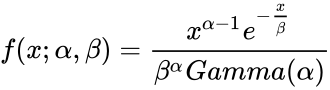 , for
, for
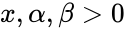 , where
, where 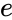 is the natural number(e = 2.71828...),
is the natural number(e = 2.71828...), 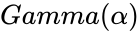 is the Gamma function.
is the Gamma function.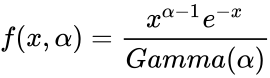 .
.
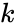 .
.