Difference between revisions of "Manuals/calci/GAMMALN"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*Normally the number <math>e</math> to the power <math>GAMMALN(x)</math>, where <math>x</math> is an integer, is same as <math>(x-1)!</math>. | *Normally the number <math>e</math> to the power <math>GAMMALN(x)</math>, where <math>x</math> is an integer, is same as <math>(x-1)!</math>. | ||
:<math>GAMMALN=LN(GAMMA(x))</math>, | :<math>GAMMALN=LN(GAMMA(x))</math>, | ||
| − | + | where | |
: <math>GAMMA(x) = \int\limits_{0}^{\infty} t^{x-1} e^{-t} dt</math> | : <math>GAMMA(x) = \int\limits_{0}^{\infty} t^{x-1} e^{-t} dt</math> | ||
it is for all complex numbers except the negative integers and zero. | it is for all complex numbers except the negative integers and zero. | ||
Revision as of 04:41, 4 December 2013
GAMMALN(x)
- is the number
Description
- This function gives the natural logarithm of the absolute value of the Gamma Function.
- The functions Digamma and Trigamma are the first and second derivatives of the logarithm of the Gamma Function.
- This is often called the ‘Polygamma’ function.
- Gamma, Lgamma, Digamma and Trigamma functions are internal generic primitive functions.
- Normally the number to the power , where is an integer, is same as .
- ,
where
it is for all complex numbers except the negative integers and zero.
- This function will give the result as error when
is non-numeric and .
Examples
- GAMMALN(6) = 4.787491744416229
- GAMMALN(42) = 114.03421178146174
- GAMMALN(1) = 0.00018319639111644828(calci)
- GAMMALN(-10) = NAN, because
 is the number
is the number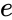 to the power
to the power 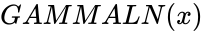 , where
, where 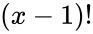 .
. ,
,
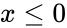 .
.