Difference between revisions of "Manuals/calci/GEOMEAN"
Jump to navigation
Jump to search
| Line 2: | Line 2: | ||
*<math>n1,n2</math> are the positive real numbers. | *<math>n1,n2</math> are the positive real numbers. | ||
==Description== | ==Description== | ||
| − | *This function gives the | + | *This function gives the Geometric Mean of an array or references. |
| − | *For example it is used to calculate average rate of growth of human population. | + | *For example, it is used to calculate average rate of growth of human population. |
| − | *The | + | *The Geometric Mean of two numbers is, the square root of their product. |
| − | *So the geometric mean of n numbers is defined as the | + | *The Geometric Mean of the three numbers is, the cube root of their product. |
| − | *In GEOMEAN(n1,n2...)n1,n2.. | + | *So the geometric mean of <math>n</math> numbers is defined as the <math>n^{th}</math> root of the product of the numbers. |
| − | *The arguments can be numbers ,names, arrays or references that contain numbers. | + | *In <math>GEOMEAN(n1,n2...)</math>, <math>n1,n2...</math> are the positive real numbers and <math>n1</math> is required. <math>n2,n3...</math> are optional. |
| + | *The arguments can be numbers,names,arrays or references that contain numbers. | ||
*Also we can directly use logical values and text representations of numbers. | *Also we can directly use logical values and text representations of numbers. | ||
| − | *The values are ignored when the argument contains logical values or empty cells. | + | *The values are ignored, when the argument contains logical values or empty cells. |
| − | *The | + | *The Geometric and Arithmetic Means are equal, when all the numbers in the given set are equal, otherwise the Geometric Mean of a data set is less than the data set's Arithmetic Mean. |
*The geometric mean of a data set {a1,a2 ...,an} is given by: | *The geometric mean of a data set {a1,a2 ...,an} is given by: | ||
| − | + | <math>{\prod_{i=1}^n ai}^{\frac{1}{n}} = \sqrt[n]{a1, a2 ... an}</math> | |
*This function will give the result as error when | *This function will give the result as error when | ||
| − | + | 1.Any one of the argument is non-numeric | |
| − | + | 2.Any one <math>value \le 0</math> | |
| − | + | 3.Any one of the references cannot be translated in to numbers. | |
==Examples== | ==Examples== | ||
Revision as of 00:24, 5 December 2013
GEOMEAN(n1,n2,…)
- are the positive real numbers.
Description
- This function gives the Geometric Mean of an array or references.
- For example, it is used to calculate average rate of growth of human population.
- The Geometric Mean of two numbers is, the square root of their product.
- The Geometric Mean of the three numbers is, the cube root of their product.
- So the geometric mean of numbers is defined as the root of the product of the numbers.
- In , are the positive real numbers and is required. are optional.
- The arguments can be numbers,names,arrays or references that contain numbers.
- Also we can directly use logical values and text representations of numbers.
- The values are ignored, when the argument contains logical values or empty cells.
- The Geometric and Arithmetic Means are equal, when all the numbers in the given set are equal, otherwise the Geometric Mean of a data set is less than the data set's Arithmetic Mean.
- The geometric mean of a data set {a1,a2 ...,an} is given by:
- This function will give the result as error when
1.Any one of the argument is non-numeric 2.Any one 3.Any one of the references cannot be translated in to numbers.
Examples
- GEOMEAN(3,27)=9
- GEOMEAN(2,4,8)=4
- GEOMEAN(3,5,8,10,12)=6.786916380543178
- GEOMEAN(-2,32)=NAN, because the value is<0.
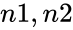 are the positive real numbers.
are the positive real numbers. numbers is defined as the
numbers is defined as the 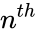 root of the product of the numbers.
root of the product of the numbers.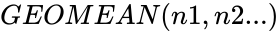 ,
, 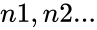 are the positive real numbers and
are the positive real numbers and  is required.
is required. 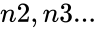 are optional.
are optional.![{\displaystyle {\prod _{i=1}^{n}ai}^{\frac {1}{n}}={\sqrt[{n}]{a1,a2...an}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/ec8ebe373ef4b3758c7640d0f333a40e3e7d0550)
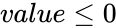 3.Any one of the references cannot be translated in to numbers.
3.Any one of the references cannot be translated in to numbers.