Difference between revisions of "Manuals/calci/FISHER"
Jump to navigation
Jump to search
| Line 13: | Line 13: | ||
==Examples== | ==Examples== | ||
| − | #FISHER(0.5642)=0.6389731838284958 | + | #FISHER(0.5642) = 0.6389731838284958 |
| − | #FISHER(0)=0 | + | #FISHER(0)= 0 |
| − | #FISHER(-0.3278)=-0.3403614004970268 | + | #FISHER(-0.3278) = -0.3403614004970268 |
| − | #FISHER(1)=Infinity | + | #FISHER(1) = Infinity |
| − | #FISHER(-1)=Infinity | + | #FISHER(-1) = Infinity |
==See Also== | ==See Also== | ||
Revision as of 00:03, 10 December 2013
FISHER(x)
- is the number.
Description
- This function gives the value of Fisher Transformation at .
- Fisher Transformation is used to test the hypothesis of two correlations.
- It is mainly associated with the Pearson Product-Moment Correlation coefficient for bi-variate normal observations.
- In , is the number which ranges between -1 to +1.
- The transformation is defined by : , where is the natural logarithm function and is the Inverse Hyperbolic function.
- This function will give the result as error when:
1. is non-numeric 2. or <math>x\ge<math> .
Examples
- FISHER(0.5642) = 0.6389731838284958
- FISHER(0)= 0
- FISHER(-0.3278) = -0.3403614004970268
- FISHER(1) = Infinity
- FISHER(-1) = Infinity
See Also
 is the number.
is the number.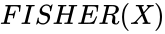 ,
, 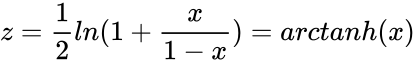 , where
, where 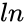 is the natural logarithm function and
is the natural logarithm function and 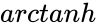 is the Inverse Hyperbolic function.
is the Inverse Hyperbolic function.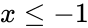 or <math>x\ge<math> .
or <math>x\ge<math> .