Difference between revisions of "Manuals/calci/INTERCEPT"
| Line 9: | Line 9: | ||
*It is fits a straight line through the set of <math> n </math> points in such a way that makes vertical distances between the points of the data set and the fitted line as small as possible. | *It is fits a straight line through the set of <math> n </math> points in such a way that makes vertical distances between the points of the data set and the fitted line as small as possible. | ||
*Regression methods nearly to the simple ordinary least squares also exist. | *Regression methods nearly to the simple ordinary least squares also exist. | ||
| − | *i.e.,The Least Squares method relies on taking partial derivatives with respect to the slope | + | *i.e.,The Least Squares method relies on taking partial derivatives with respect to the slope and intercept which provides a solvable pair of equations called normal equations. |
| − | and intercept which provides a solvable pair of equations called normal equations. | ||
*Suppose there are <math> n </math> data points <math> {y_{i}, x_{i}}</math>, where i = 1, 2, …, n. | *Suppose there are <math> n </math> data points <math> {y_{i}, x_{i}}</math>, where i = 1, 2, …, n. | ||
| − | *To find the equation of the regression line:<math> a=bar{y}-b.bar{x}</math>. | + | *To find the equation of the regression line:<math> a=\bar{y}-b.\bar{x}</math>. |
*This equation will give a "best" fit for the data points. | *This equation will give a "best" fit for the data points. | ||
*The "best" means least-squares method. Here b is the slope. | *The "best" means least-squares method. Here b is the slope. | ||
| − | *The slope is calculated by:<math> b=\frac{\sum_{i=1}^{n} {(x_{i}-\bar{x})(y_{i}-\bar{y})}} {\sum_{i=1}^{n}{(x_{i}-bar{x})}^2}</math>. | + | *The slope is calculated by:<math> b=\frac{\sum_{i=1}^{n} {(x_{i}-\bar{x})(y_{i}-\bar{y})}} {\sum_{i=1}^{n}{(x_{i}-\bar{x})}^2}</math>. |
| − | *In this formula<math> bar{x}</math> and<math> bar{y}</math> are the sample means AVERAGE of <math> x</math> and <math> y </math>. | + | *In this formula<math> \bar{x}</math> and<math> \bar{y}</math> are the sample means AVERAGE of <math> x</math> and <math> y </math>. |
*In <math>INTERCEPT(y,x)</math> , the arguments can be numbers, names, arrays, or references that contain numbers. | *In <math>INTERCEPT(y,x)</math> , the arguments can be numbers, names, arrays, or references that contain numbers. | ||
* The arrays values are disregarded when it is contains text, logical values or empty cells. | * The arrays values are disregarded when it is contains text, logical values or empty cells. | ||
Revision as of 23:58, 18 December 2013
- is the set of dependent data
- is the set of independent data.
Description
- This function is calculating the point where the line is intesecting y-axis using dependent and independent variables.
- Using this function we can find the value of when is zero.
- The intercept point is finding using simple linear regression.
- It is fits a straight line through the set of points in such a way that makes vertical distances between the points of the data set and the fitted line as small as possible.
- Regression methods nearly to the simple ordinary least squares also exist.
- i.e.,The Least Squares method relies on taking partial derivatives with respect to the slope and intercept which provides a solvable pair of equations called normal equations.
- Suppose there are data points , where i = 1, 2, …, n.
- To find the equation of the regression line:.
- This equation will give a "best" fit for the data points.
- The "best" means least-squares method. Here b is the slope.
- The slope is calculated by:.
- In this formula and are the sample means AVERAGE of and .
- In , the arguments can be numbers, names, arrays, or references that contain numbers.
- The arrays values are disregarded when it is contains text, logical values or empty cells.
- This function will return the result as error when any one of the argument is nonnueric or x and y is having different number of data points and there is no data.
INTERCEPT(Y,X)
Where Y is the dependent set of observations or data, and
Y is the independent set of observations or data.
This function calculates the point at which a line will intersect the y-axis using the available x-values and y-values.
· An array contains text, logical values, or empty cells that are ignored; but, the cells with the value zero are included.
· INTERCEPT shows the error value, when Y and X have a dissimilar number of data points.
Formulas:-
· The equation to calculate the intercept of the regression line, a, is:
where b is the slope, and is calculated as:
and where x and y are the sample means AVERAGE(Y) and AVERAGE(X).
INTERCEPT
Lets see an example,
INTERCEPT(Y, X)
B C
10 13
8 11
15 18
6 12
12 10
=INTERCEPT(B2:B6,C2:C6) is 1.2268
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 10 | 13 | 1.226804 | |
| Row2 | 8 | 11 | ||
| Row3 | 15 | 18 | ||
| Row4 | 6 | 12 | ||
| Row5 | 12 | 10 | ||
| Row6 |
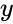 is the set of dependent data
is the set of dependent data is the set of independent data.
is the set of independent data. points in such a way that makes vertical distances between the points of the data set and the fitted line as small as possible.
points in such a way that makes vertical distances between the points of the data set and the fitted line as small as possible.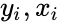 , where i = 1, 2, …, n.
, where i = 1, 2, …, n.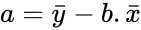 .
.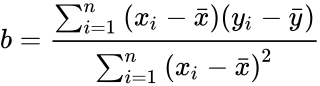 .
.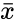 and
and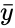 are the sample means AVERAGE of
are the sample means AVERAGE of 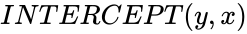 , the arguments can be numbers, names, arrays, or references that contain numbers.
, the arguments can be numbers, names, arrays, or references that contain numbers.