Difference between revisions of "Manuals/calci/IMREAL"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
==Description== | ==Description== | ||
*This function gives the real coefficient of the complex number. | *This function gives the real coefficient of the complex number. | ||
| − | *IMREAL(z), | + | *IMREAL(z), <math>z</math> is the complex number is in the form of <math>x+iy</math> |
* where <math>x</math> & <math>y</math> are the real numbers. <math>i</math> imaginary unit. <math>i=sqrt{-1}</math>. | * where <math>x</math> & <math>y</math> are the real numbers. <math>i</math> imaginary unit. <math>i=sqrt{-1}</math>. | ||
*The complex number <math>z= x+iy</math> can be identified by <math>(x,y)</math> in the complex plane. | *The complex number <math>z= x+iy</math> can be identified by <math>(x,y)</math> in the complex plane. | ||
Revision as of 00:18, 20 December 2013
IMREAL(z)
- is the complex number is of the form
Description
- This function gives the real coefficient of the complex number.
- IMREAL(z), is the complex number is in the form of
- where & are the real numbers. imaginary unit. .
- The complex number can be identified by in the complex plane.
- Here is called real part and </math>y</math> is the imaginary part of .
- This function shows the value of the real part of .
- A complex is said to be purely imaginary when and it is a real number when .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMREAL("3+4i")=3
- IMREAL("-5+6i")=-5
- IMREAL("8")=8
- IMREAL("-2i")=0
See Also
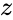 is the complex number is of the form
is the complex number is of the form 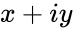
 &
& 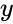 are the real numbers.
are the real numbers. 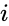 imaginary unit.
imaginary unit. 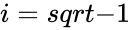 .
.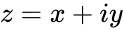 can be identified by
can be identified by 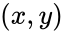 in the complex plane.
in the complex plane.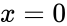 and it is a real number when
and it is a real number when 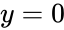 .
.