Difference between revisions of "Manuals/calci/SLOPE"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
==Description== | ==Description== | ||
*This function gives the slope of the linear regression line through a set of given points. | *This function gives the slope of the linear regression line through a set of given points. | ||
| − | *The slope of a regression line (b) represents the rate of change in y as x changes. | + | *The slope of a regression line (b) represents the rate of change in <math> y </math> as ,math> x </math> changes. |
*To find a slope we can use the least squares method. | *To find a slope we can use the least squares method. | ||
*Slope is found by calculating b as the covariance of x and y, divided by the sum of squares (variance) of x. | *Slope is found by calculating b as the covariance of x and y, divided by the sum of squares (variance) of x. | ||
| − | *In SLOPE(y,x), y is the array of the numeric dependent values and x is the array of the independent values. | + | *In <math>SLOPE(y,x), y </math> is the array of the numeric dependent values and <math> x </math> is the array of the independent values. |
*The arguments can be be either numbers or names, array,constants or references that contain numbers. | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | ||
*Suppose the array contains text,logical values or empty cells, like that values are not considered. | *Suppose the array contains text,logical values or empty cells, like that values are not considered. | ||
| − | *The equation for the slope of the regression line is :<math>b = \frac {\sum (x-\bar{x})(y-\bar{y})} {\sum(x-\bar{x})^2</math>. where <math>\bar{x}</math> and <math>\bar{y}</math> are the sample mean x and y. | + | *The equation for the slope of the regression line is :<math>b = \frac {\sum (x-\bar{x})(y-\bar{y})} {\sum(x-\bar{x})^2}</math>. where <math>\bar{x}</math> and <math>\bar{y}</math> are the sample mean x and y. |
*This function will return the result as error when | *This function will return the result as error when | ||
1. Any one of the argument is nonnumeric. | 1. Any one of the argument is nonnumeric. | ||
Revision as of 03:13, 20 January 2014
SLOPE(y,x)
- is the set of dependent values.
- is the set of independent values.
Description
- This function gives the slope of the linear regression line through a set of given points.
- The slope of a regression line (b) represents the rate of change in as ,math> x </math> changes.
- To find a slope we can use the least squares method.
- Slope is found by calculating b as the covariance of x and y, divided by the sum of squares (variance) of x.
- In is the array of the numeric dependent values and is the array of the independent values.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logical values or empty cells, like that values are not considered.
- The equation for the slope of the regression line is :. where and are the sample mean x and y.
- This function will return the result as error when
1. Any one of the argument is nonnumeric. 2. x and y are empty or that have a different number of data points.
Examples
1.y={4,9,2,6,7}
x={1,5,10,3,4}
SLOPE(A1:A5,B1:B5)=-0.305309734513 2.y={2,9,3,8,10,17}
x={4,5,11,7,15,12}
SLOPE(B1:B6,C1:C6)=0.58510638297 3.y={0,9,4}
x={-1,5,7}
SLOPE(C1:C3)=0.730769230769
See Also
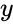 is the set of dependent values.
is the set of dependent values. is the set of independent values.
is the set of independent values.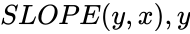 is the array of the numeric dependent values and
is the array of the numeric dependent values and 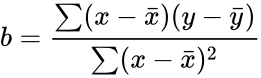 . where
. where 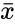 and
and 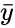 are the sample mean x and y.
are the sample mean x and y.