Difference between revisions of "Manuals/calci/SKEW"
Jump to navigation
Jump to search
| Line 41: | Line 41: | ||
! 5 | ! 5 | ||
| 4 || 5 || 9 ||78 || 6 | | 4 || 5 || 9 ||78 || 6 | ||
| + | |- | ||
! 6 | ! 6 | ||
| 38 || 9 || 13 ||48 || 11 | | 38 || 9 || 13 ||48 || 11 | ||
|} | |} | ||
1.Array={4,9,11,10,5} | 1.Array={4,9,11,10,5} | ||
| − | SKEW(B1:B5)=-0.4369344921493 | + | =SKEW(B1:B5)=-0.4369344921493 |
2.Array={0,29,41,18,4,38} | 2.Array={0,29,41,18,4,38} | ||
| − | SKEW(A1:A6)=-0.21921252920 | + | =SKEW(A1:A6)=-0.21921252920 |
3.Array={-5,11,18,7} | 3.Array={-5,11,18,7} | ||
| − | SKEW(C1:C4)=-0.715957010 | + | =SKEW(C1:C4)=-0.715957010 |
4.Array={4,5,2,5,6,8} | 4.Array={4,5,2,5,6,8} | ||
| − | SKEW(C1:C6)=0 | + | =SKEW(C1:C6)=0 |
5.Array={1,2,3,5,6,11} | 5.Array={1,2,3,5,6,11} | ||
| − | SKEW(E1:E6)=1.16584702768 | + | =SKEW(E1:E6)=1.16584702768 |
==See Also== | ==See Also== | ||
Revision as of 06:39, 21 January 2014
SKEW(n1,n2,…)
- Failed to parse (syntax error): {\displaystyle n_1,n_2,…} are numbers to calculate the skewness.
Description
- This function gives the Skewness of a distribution.
- Skewness is a measure of the degree of asymmetry of a distribution.
- A distribution(normal distribution) is symmetry ,it don't have a Skewness.
- In a distribution the left tail is more pronounced than the right tail (towards more negative values) then the function is said to have Negative Skewness.
- If a distribution is skewed to the right, the tail on the curve's right-hand side is longer than the tail on the left-hand side (towards more positive values), then the function is said to have a positive skewness.
- In a Left Skewed Distribution, its
- In a Normal Skewed Distribution, its
- In a Right Skewed Distribution, its .
- In is required. are optional.
- In calci there is no restriction for giving the number of arguments.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logicl values or empty cells, like that values are not considered.
- The equation for Skewness is defined by :
Where, is the sample standard deviation, represents a sample mean.
- This function will return the result as error when
1. Any one of the argument is non-numeric. 2. If there are fewer than three data points, or the Sample Standard Deviation is zero.
Examples
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 0 | 4 | -5 | 9 | 1 |
| 2 | 29 | 9 | 11 | 20 | 2 |
| 3 | 41 | 11 | 18 | 6 | 3 |
| 4 | 18 | 10 | 7 | 42 | 5 |
| 5 | 4 | 5 | 9 | 78 | 6 |
| 6 | 38 | 9 | 13 | 48 | 11 |
1.Array={4,9,11,10,5} =SKEW(B1:B5)=-0.4369344921493 2.Array={0,29,41,18,4,38} =SKEW(A1:A6)=-0.21921252920 3.Array={-5,11,18,7} =SKEW(C1:C4)=-0.715957010 4.Array={4,5,2,5,6,8} =SKEW(C1:C6)=0 5.Array={1,2,3,5,6,11} =SKEW(E1:E6)=1.16584702768
See Also
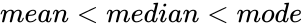
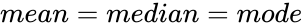
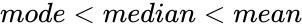 .
.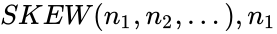 is required.
is required.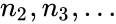 are optional.
are optional.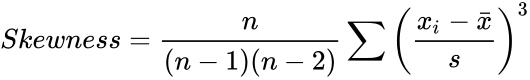
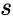 is the sample standard deviation,
is the sample standard deviation, 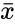 represents a sample mean.
represents a sample mean.