Difference between revisions of "Manuals/calci/HANKEL"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''HANKEL'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''HANKEL'''</div><br/> | <div style="font-size:30px">'''HANKEL'''</div><br/> | ||
| + | <div style="font-size:30px">'''MATRIX("HANKEL",order)'''</div><br/> | ||
| + | *<math>order</math> is the order of the hankel matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the matrix with the property of hankel matrix. | ||
| + | *A hankel matrix is a square matrix with constant skew diagonals. | ||
| + | *If the i,j element of Hankel matrix A is denoted <math>A_{i,j}</math>, then we have | ||
| + | <math>A_{i,j} = A_{i-1,j+1}</math>. | ||
| + | *i.e., The form of Hankel matrix is: | ||
| + | <math>\begin{bmatrix} | ||
| + | a & b & c & d & e \\ | ||
| + | b & c & d & e & f \\ | ||
| + | c & d & e & f & g \\ | ||
| + | d & e & f & g & h \\ | ||
| + | e & f & g & h & i \\ | ||
| + | \end{bmatrix}</math>. | ||
| + | *A hankel matrix is also called as catalecticant matrix. | ||
| + | *Here MATRIX("hankel") is gives the hankel matrix of order 3 with decimal values. | ||
| + | *A Hankel matrix is an upside-down Toeplitz matrix. | ||
| + | *A matrix whose entries along a parallel to the main anti-diagonal are equal, for each parallel. | ||
| + | *Equivalently, is a Hankel matrix if and only if there exists a sequence, such that ,If are square matrices, then is referred to as a block Hankel matrix. | ||
| + | |||
| + | ==Examples== | ||
| + | #MATRIX("hankel") | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0.6414852568414062 || 0.9679132911842316 || 0.6076015164144337 | ||
| + | |- | ||
| + | | 0.9679132911842316 || 0.6076015164144337 || 0.6414852568414062 | ||
| + | |- | ||
| + | | 0.6076015164144337 || 0.6414852568414062 || 0.9679132911842316 | ||
| + | |} | ||
Revision as of 10:01, 24 April 2015
HANKEL
MATRIX("HANKEL",order)
- is the order of the hankel matrix.
Description
- This function gives the matrix with the property of hankel matrix.
- A hankel matrix is a square matrix with constant skew diagonals.
- If the i,j element of Hankel matrix A is denoted , then we have
.
- i.e., The form of Hankel matrix is:
.
- A hankel matrix is also called as catalecticant matrix.
- Here MATRIX("hankel") is gives the hankel matrix of order 3 with decimal values.
- A Hankel matrix is an upside-down Toeplitz matrix.
- A matrix whose entries along a parallel to the main anti-diagonal are equal, for each parallel.
- Equivalently, is a Hankel matrix if and only if there exists a sequence, such that ,If are square matrices, then is referred to as a block Hankel matrix.
Examples
- MATRIX("hankel")
| 0.6414852568414062 | 0.9679132911842316 | 0.6076015164144337 |
| 0.9679132911842316 | 0.6076015164144337 | 0.6414852568414062 |
| 0.6076015164144337 | 0.6414852568414062 | 0.9679132911842316 |
 is the order of the hankel matrix.
is the order of the hankel matrix.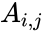 , then we have
, then we have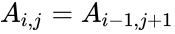 .
.
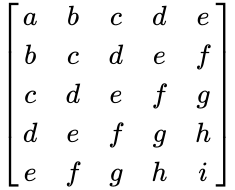 .
.