Difference between revisions of "Manuals/calci/IDEMPOTENT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''IDEMPOTENT'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IDEMPOTENT'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("IDEMPOTENT",order)'''</div><br/> |
| + | *<math>order</math> is the size of the Idempotent matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function is showing the idempotent matrix of order 3. | ||
| + | *An idempotent matrix is a matrix which, when multiplied by itself, is getting the same matrix. | ||
| + | *i.e.,A square matrix K is said to be idempotent if <math>K^2=K</math>. | ||
| + | *The properties of idempotent matrix is: | ||
| + | # <math>K^r=K</math> for r being a positive integer. | ||
| + | # I-K is idempotent. | ||
| + | # If <math>K_1</math> and <math>K_2</math> are idempotent matrices and <math>K_1K_2 =K_2K_1</math>. Then <math>K_1K_2</math> is idempotent. | ||
Revision as of 13:28, 5 May 2015
MATRIX("IDEMPOTENT",order)
- is the size of the Idempotent matrix.
Description
- This function is showing the idempotent matrix of order 3.
- An idempotent matrix is a matrix which, when multiplied by itself, is getting the same matrix.
- i.e.,A square matrix K is said to be idempotent if .
- The properties of idempotent matrix is:
- for r being a positive integer.
- I-K is idempotent.
- If and are idempotent matrices and . Then is idempotent.
 is the size of the Idempotent matrix.
is the size of the Idempotent matrix.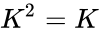 .
.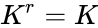 for r being a positive integer.
for r being a positive integer.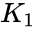 and
and  are idempotent matrices and
are idempotent matrices and 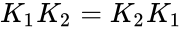 . Then
. Then 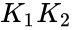 is idempotent.
is idempotent.