Difference between revisions of "Manuals/calci/FTESTANALYSIS"
Jump to navigation
Jump to search
| Line 31: | Line 31: | ||
==Examples== | ==Examples== | ||
| + | 1. | ||
{| class="wikitable" | {| class="wikitable" | ||
|+Spreadsheet | |+Spreadsheet | ||
| Line 48: | Line 49: | ||
|32 || 11 | |32 || 11 | ||
|} | |} | ||
| − | FTESTANALYSIS(A1:A4,B1:B4,0.5,TRUE) | + | =FTESTANALYSIS(A1:A4,B1:B4,0.5,TRUE) |
{| class="wikitable" | {| class="wikitable" | ||
| Line 71: | Line 72: | ||
2. | 2. | ||
| − | {| class="wikitable" | + | {| class="wikitable" |
| − | + | |+Spreadsheet | |
| − | + | |- | |
| − | + | ! !! A !! B | |
| − | + | |- | |
| − | + | ! 1 | |
| − | + | |5 || 10 | |
| − | + | |- | |
| + | ! 2 | ||
| + | |8 || 20 | ||
| + | |- | ||
| + | ! 3 | ||
| + | |12 || 30 | ||
| + | |- | ||
| + | ! 4 | ||
| + | |45 || 40 | ||
| + | |- | ||
| + | ! 5 | ||
| + | |23 || 50 | ||
|} | |} | ||
| + | =FTEST(A1:A5,B1:B5,0.30,false) | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | + | |- | |
| − | + | ! !!Variable1 !! Variable2 | |
| − | + | |- | |
| − | + | | Mean || 18.6 || 30 | |
| − | + | |- | |
| − | + | | Variance || 264.29999999999995 || 250 | |
| − | + | |- | |
| − | | | + | | Observations || 5 || 5 |
| − | + | |- | |
| − | + | | Degree Of Freedom || 4 || 4 | |
| − | + | |- | |
| − | + | | F-Value || 1.0572 || | |
| − | + | |- | |
| − | + | | P(F<=f) one-tail || 0.4791517866106137 || | |
| − | + | |- | |
| − | + | | F Critical one-tail || 1.7528541706121352 || | |
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | |||
==See Also== | ==See Also== | ||
Revision as of 09:55, 3 June 2015
FTESTANALYSIS(ar1,ar2,alpha,newtableflag)
- and are array of data.
- is the significance level.
- is the logical value.
Description
- This function gives the analysis of variance.
- This statistics used to determine the significant difference of three or more variables or multivariate collected from experimental
research.
- So this analysis is depending on the hypothesis.
- The hypotheses for this test are
(null hypothesis, variances are equal) (alternative hypothesis, variances are not equal)
- For example, the comparison of SCORES across GROUPS,where there are two groups.
- The purpose is to determine if the mean SCORE on a test is different for the two groups tested (i.e., control and treatment groups)
- In FTESTANALYSIS(ar1,ar2,alpha,newtableflag) where is the data of first array, is the data of second array.
- is the significance level which ranges from 0 to 1.
- is the logical value like TRUE or FALSE.
- TRUE is indicating the result will display in new worksheet.Suppose we are omitted the lv value it will consider the value as FALSE.
- The F statistic of this function calculated by:
has an F-distribution with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n−1} and Failed to parse (syntax error): {\displaystyle m−1} degrees of freedom.
- Also is the sample variance of first set of values.
- And is the sample variance of second set of values.
- If the f-value from the test is higher than the f-critical value then the null hypothesis should be rejected and the variances are unequal.
- So the following cases will occur:
- If the variances are assumed to NOT be equal, proceed with the t-test that assumes non-equal variances.
- If the variances are assumed to be equal, proceed with the t-test that assumes equal variances.
- In this function the array may be any numbers, names, or references that contains numbers.
- values are not considered if the array contains any text, logical values or empty cells.
When the or is less than 2 or the variance of the array value is zero, then this function will return the result as error.
Examples
1.
| A | B | |
|---|---|---|
| 1 | 15 | 21 |
| 2 | 27 | 12 |
| 3 | 19 | 30 |
| 4 | 32 | 11 |
=FTESTANALYSIS(A1:A4,B1:B4,0.5,TRUE)
| Variable1 | Variable2 | |
|---|---|---|
| Mean | 23.25 | 18.5 |
| Variance | 58.916666666666664 | 79 |
| Observations | 4 | 4 |
| Degree Of Freedom | 3 | 3 |
| F-Value | 0.7457805907172995 | |
| P(F<=f) one-tail | 0.407624533735915 | |
| F Critical one-tail | 1 |
2.
| A | B | |
|---|---|---|
| 1 | 5 | 10 |
| 2 | 8 | 20 |
| 3 | 12 | 30 |
| 4 | 45 | 40 |
| 5 | 23 | 50 |
=FTEST(A1:A5,B1:B5,0.30,false)
| Variable1 | Variable2 | |
|---|---|---|
| Mean | 18.6 | 30 |
| Variance | 264.29999999999995 | 250 |
| Observations | 5 | 5 |
| Degree Of Freedom | 4 | 4 |
| F-Value | 1.0572 | |
| P(F<=f) one-tail | 0.4791517866106137 | |
| F Critical one-tail | 1.7528541706121352 |
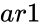 and
and 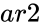 are array of data.
are array of data.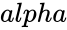 is the significance level.
is the significance level.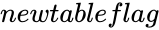 is the logical value.
is the logical value.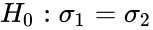 (null hypothesis, variances are equal)
(null hypothesis, variances are equal)
 (alternative hypothesis, variances are not equal)
(alternative hypothesis, variances are not equal)
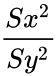 has an F-distribution with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n−1}
and Failed to parse (syntax error): {\displaystyle m−1}
degrees of freedom.
has an F-distribution with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n−1}
and Failed to parse (syntax error): {\displaystyle m−1}
degrees of freedom.
 is the sample variance of first set of values.
is the sample variance of first set of values. is the sample variance of second set of values.
is the sample variance of second set of values.