Difference between revisions of "Manuals/calci/BETAINV"
Jump to navigation
Jump to search
| Line 18: | Line 18: | ||
4.we are not mentioning the limit values for <math>a</math>&<math>b</math>, | 4.we are not mentioning the limit values for <math>a</math>&<math>b</math>, | ||
by default it will consider the Standard Cumulative Beta Distribution, a = 0 and b = 1 | by default it will consider the Standard Cumulative Beta Distribution, a = 0 and b = 1 | ||
| + | |||
| + | ==ZOS== | ||
| + | |||
| + | *The syntax is to calculate of this function in ZOS is <math>BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy)</math>. | ||
| + | **<math>probability</math> is the probability value associated with the beta distribution. | ||
| + | **<math>alpha</math> and <math>beta</math> are the values of the shape parameter. | ||
| + | **For e.g.,BETAINV(0.30987,10,18,12,16) | ||
==Examples== | ==Examples== | ||
Revision as of 11:52, 4 June 2015
BETAINV(prob,alpha,beta,a,b)
- is the probability value associated with the beta distribution.
- & are the values of the shape parameter.
- & the lower and upper limit to the interval of .
Description
- This function gives the inverse value of Cumulative Beta Probability Distribution.
- It is called Inverted Beta Function or Beta Prime.
- In , is the probability value associated with Beta Distribution, and are the values of two positive shape parameters and and are the lower and upper limit.
- Normally the limit values are optional, i.e. when we are giving the values of & then the result value is from and .
- When we are omitting the values and , by default it will consider and , so the result value is from and .
- If , then .
- use the iterating method to find the value of .suppose the iteration has not converged after 100 searches, then the function gives the error result.
- This function will give the error result when
1.Any one of the arguments are non-numeric 2. or 3. or a = b 4.we are not mentioning the limit values for &, by default it will consider the Standard Cumulative Beta Distribution, a = 0 and b = 1
ZOS
- The syntax is to calculate of this function in ZOS is .
- is the probability value associated with the beta distribution.
- and are the values of the shape parameter.
- For e.g.,BETAINV(0.30987,10,18,12,16)
Examples
- BETAINV(0.2060381025,5,9,2,6) = 3
- BETAINV(0.359492343,8,10) = 1.75
- BETAINV(0.685470581,5,8,2,6) = 3.75
- BETAINV(0.75267,1,7,7,9) = 7.25
- BETAINV(0.5689,-2,4,3,5) = NAN, because .
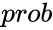 is the probability value associated with the beta distribution.
is the probability value associated with the beta distribution.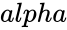 &
&  are the values of the shape parameter.
are the values of the shape parameter. &
& 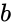 the lower and upper limit to the interval of
the lower and upper limit to the interval of  .
.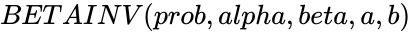 ,
, 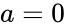 and
and 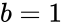 , so the result value is from
, so the result value is from 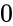 and
and  .
.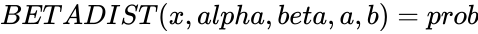 , then
, then 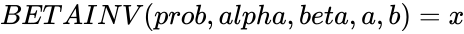 .
. use the iterating method to find the value of
use the iterating method to find the value of 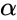 or
or 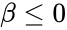 3.
3.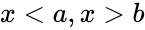 or a = b
4.we are not mentioning the limit values for
or a = b
4.we are not mentioning the limit values for 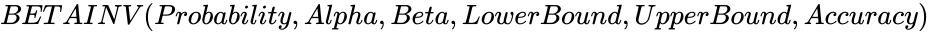 .
.
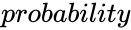 is the probability value associated with the beta distribution.
is the probability value associated with the beta distribution.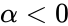 .
.