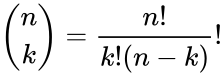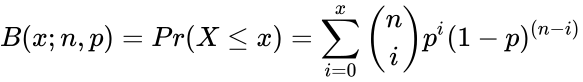Difference between revisions of "Manuals/calci/BINOMIALDISTRIBUTED"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*This gives the discrete probability distribution. | *This gives the discrete probability distribution. | ||
*The probability of getting exactly k successes in n trials is given by the Probability Mass Function: | *The probability of getting exactly k successes in n trials is given by the Probability Mass Function: | ||
| + | <math> b(k;n,p)=Pr(X = k) = \binom{n}{k}p^{k}(1-p)^{n-k}</math> for k=0,1,2,3...n where <math>\binom{n}{k}</math> is the COMBIN(n,k) i.e.<math> \binom{n}{k} = \frac{n!}{k!(n-k)}!</math> | ||
| + | |||
| + | *The Cumulative Binomial Distribution is:<math>B(x;n,p) = Pr(X \le x) =\sum_{i=0}^x \binom{n}{i}p^{i}(1-p)^{(n-i)}</math> | ||
Revision as of 13:43, 13 December 2016
BINOMIALDISTRIBUTED (Numbers,Probability)
- is the number of variables.
- is the value from 0 to 1.
Description
- This function gives the value of the Binomial distribution.
- In , is the number of the variables and is the probability value which varies from 0 to 1.
- This gives the discrete probability distribution.
- The probability of getting exactly k successes in n trials is given by the Probability Mass Function:
for k=0,1,2,3...n where is the COMBIN(n,k) i.e.
- The Cumulative Binomial Distribution is:
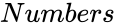 is the number of variables.
is the number of variables.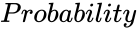 is the value from 0 to 1.
is the value from 0 to 1.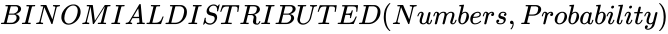 ,
, 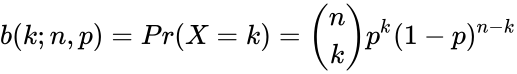 for k=0,1,2,3...n where
for k=0,1,2,3...n where 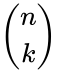 is the COMBIN(n,k) i.e.
is the COMBIN(n,k) i.e.