Difference between revisions of "Manuals/calci/BINOMIALSERIES"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*BinomialSeries is also called Maclaurin series for the function f given by <math> f(x)=(1+x)^{\alpha}</math> and <math>\alpha</math> is belongs to any Complex number. | *BinomialSeries is also called Maclaurin series for the function f given by <math> f(x)=(1+x)^{\alpha}</math> and <math>\alpha</math> is belongs to any Complex number. | ||
*In <math>BINOMIALSERIES(N,X,Y)</math>,<math>N</math> is any positive integer and x and y are any real numbers. | *In <math>BINOMIALSERIES(N,X,Y)</math>,<math>N</math> is any positive integer and x and y are any real numbers. | ||
| − | *If k is any number and |x|<1 then,<math>(1+x)^k= \sum_{n=0}^\infty \binom{k}{n} x^n</math> http://tutorial.math.lamar.edu/Classes/CalcII/BinomialSeries.aspx.So similar to the binomial theorem except that it’s an infinite series and we must have in order to get convergence. | + | *If k is any number and |x|<1 then,<math>(1+x)^k= \sum_{n=0}^\infty \binom{k}{n} x^n</math> where<math> \binom{k}{n} = \frac{k(k-1)(k-2)...(k-n+1)}{n!} </math>,n=1,2,3...http://tutorial.math.lamar.edu/Classes/CalcII/BinomialSeries.aspx. |
| + | *So similar to the binomial theorem except that it’s an infinite series and we must have in order to get convergence. | ||
*This function will give the result as error when | *This function will give the result as error when | ||
#1. N is not positive number. | #1. N is not positive number. | ||
#2. N,X and Y is a Non-numeric. | #2. N,X and Y is a Non-numeric. | ||
Revision as of 14:27, 13 December 2016
BINOMIALSERIES (N,X,Y)
- are any real numbers.
Description
- This function gives the coefficient of the Binomial series.
- BinomialSeries is also called Maclaurin series for the function f given by and is belongs to any Complex number.
- In , is any positive integer and x and y are any real numbers.
- If k is any number and |x|<1 then, where,n=1,2,3...http://tutorial.math.lamar.edu/Classes/CalcII/BinomialSeries.aspx.
- So similar to the binomial theorem except that it’s an infinite series and we must have in order to get convergence.
- This function will give the result as error when
- 1. N is not positive number.
- 2. N,X and Y is a Non-numeric.
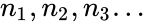 are any real numbers.
are any real numbers.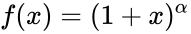 and
and 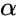 is belongs to any Complex number.
is belongs to any Complex number.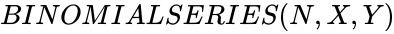 ,
,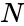 is any positive integer and x and y are any real numbers.
is any positive integer and x and y are any real numbers.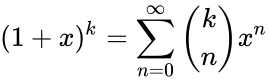 where
where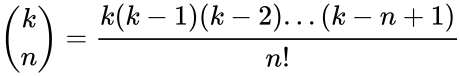 ,n=1,2,3...
,n=1,2,3...