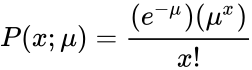Difference between revisions of "Manuals/calci/POISSONDISTRIBUTED"
Jump to navigation
Jump to search
(Created page with "poisson") |
|||
| Line 1: | Line 1: | ||
| − | poisson | + | <div style="font-size:30px">'''POISSONDISTRIBUTED(Numbers,Lambda)'''</div><br/> |
| + | *<math>Numbers</math> is the number of random numbers to display. | ||
| + | *<math>Lamda</math> is the mean value. | ||
| + | |||
| + | ==Description== | ||
| + | *This function shows the random variables of Poisson distribution. | ||
| + | *It is a discrete frequency distribution which gives the probability of a number of independent events occurring in a fixed time. | ||
| + | *A Poisson random variable is the number of successes that result from a Poisson experiment. | ||
| + | *The probability distribution of a Poisson random variable is called a Poisson distribution. | ||
| + | *Suppose we conduct a Poisson experiment, in which the average number of successes within a given region is <math>\mu</math>. | ||
| + | *Then, the Poisson probability is: | ||
| + | <math>P(x;\mu) = \frac{(e^{-\mu}) (\mu^x)}{ x!}</math> | ||
| + | *where x is the actual number of successes that result from the experiment, and e is approximately equal to 2.71828. | ||
| + | *The Poisson distribution has the following properties: | ||
| + | #The mean of the distribution is equal to <math>\mu</math> . | ||
| + | #The variance is also equal to <math>\mu</math> . | ||
| + | *This function will give the result as error when b<0 and a value is not an integer. | ||
| + | |||
| + | ==Examples== | ||
| + | #POISSONDISTRIBUTED(3,3) = 2 1 3 | ||
| + | #POISSONDISTRIBUTED(5,45) = 37 39 45 35 47 | ||
| + | #POISSONDISTRIBUTED(7,67.45) = 79.45 65.45 75.45 72.45 83.45 74.45 77.45 | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/POISSON | POISSON ]] | ||
| + | *[[Manuals/calci/EXPONDIST | EXPONDIST ]] | ||
| + | |||
| + | ==References== | ||
| + | [http://stattrek.com/probability-distributions/poisson.aspx Poisson Probability Distribution ] | ||
Revision as of 13:58, 15 December 2016
POISSONDISTRIBUTED(Numbers,Lambda)
- is the number of random numbers to display.
- is the mean value.
Description
- This function shows the random variables of Poisson distribution.
- It is a discrete frequency distribution which gives the probability of a number of independent events occurring in a fixed time.
- A Poisson random variable is the number of successes that result from a Poisson experiment.
- The probability distribution of a Poisson random variable is called a Poisson distribution.
- Suppose we conduct a Poisson experiment, in which the average number of successes within a given region is .
- Then, the Poisson probability is:
- where x is the actual number of successes that result from the experiment, and e is approximately equal to 2.71828.
- The Poisson distribution has the following properties:
- The mean of the distribution is equal to .
- The variance is also equal to .
- This function will give the result as error when b<0 and a value is not an integer.
Examples
- POISSONDISTRIBUTED(3,3) = 2 1 3
- POISSONDISTRIBUTED(5,45) = 37 39 45 35 47
- POISSONDISTRIBUTED(7,67.45) = 79.45 65.45 75.45 72.45 83.45 74.45 77.45
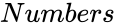 is the number of random numbers to display.
is the number of random numbers to display.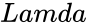 is the mean value.
is the mean value.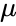 .
.