Difference between revisions of "Manuals/calci/DYADIC"
Jump to navigation
Jump to search
(Created page with "dya") |
|||
| Line 1: | Line 1: | ||
| − | + | <div style="font-size:30px">'''DYADIC(a,b)'''</div><br/> | |
| + | OR '''VECTORDIRECTPRODUCT (a,b) ''' | ||
| + | *<math> a</math> and <math>b</math> any two set of values. | ||
| + | |||
| + | ==Description== | ||
| + | *This function shows the Vector Direct product. | ||
| + | *The third type of vector multiplication is called the direct product, and is written AB. | ||
| + | *In <math>VECTORDIRECTPRODUCT (a,b)</math>, <math>a</math> and <math>b</math> are the two vectors. | ||
| + | *Multiplying one vector by another under the direct product gives a tensor result. | ||
| + | *The rectangular components of the direct product may be found by matrix multiplication: one multiplies the column vector A by the transpose of B, which gives a 3X3 matrix:<math>AB=AB^T</math>=\begin{pmatrix} | ||
| + | A_x \\ | ||
| + | A_y \\ | ||
| + | A_z | ||
| + | \end{pmatrix}method | ||
| + | *The direct product is non-commutative (AB 6D BA).A few vector product identities are of interest | ||
Revision as of 14:30, 3 March 2017
DYADIC(a,b)
OR VECTORDIRECTPRODUCT (a,b)
- and any two set of values.
Description
- This function shows the Vector Direct product.
- The third type of vector multiplication is called the direct product, and is written AB.
- In , and are the two vectors.
- Multiplying one vector by another under the direct product gives a tensor result.
- The rectangular components of the direct product may be found by matrix multiplication: one multiplies the column vector A by the transpose of B, which gives a 3X3 matrix:=\begin{pmatrix}
A_x \\ A_y \\ A_z \end{pmatrix}method
- The direct product is non-commutative (AB 6D BA).A few vector product identities are of interest
 and
and  any two set of values.
any two set of values.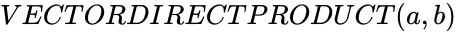 ,
, 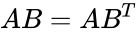 =\begin{pmatrix}
=\begin{pmatrix}