Difference between revisions of "Manuals/calci/COMPLEMENT"
Jump to navigation
Jump to search
(Created page with "complement") |
|||
| Line 1: | Line 1: | ||
| − | complement | + | <div style="font-size:30px">'''COMPLEMENT (B,A) '''</div><br/> |
| + | *<math>B</math> and <math>A</math> are any two sets. | ||
| + | |||
| + | ==Description== | ||
| + | *This function shows the complement of the given sets. | ||
| + | *In <math>COMPLEMENT (B,A)</math>, <math>B</math> and <math>A</math> are two sets. | ||
| + | *In Set theory,the complement of a set A refers to elements not in A and which will be in the set B(Universal set). | ||
| + | *So complement os A is defined by:The relative complement of A with respect to a set B, also termed the difference of sets A and B, written <math>\frac{B}{A}</math>, is the set of elements in B but not in A. | ||
| + | *When all sets under consideration are considered to be subsets of a given set U(Universal Set), the absolute complement of A is the set of elements in U but not in A. | ||
Revision as of 13:08, 5 April 2017
COMPLEMENT (B,A)
- and are any two sets.
Description
- This function shows the complement of the given sets.
- In , and are two sets.
- In Set theory,the complement of a set A refers to elements not in A and which will be in the set B(Universal set).
- So complement os A is defined by:The relative complement of A with respect to a set B, also termed the difference of sets A and B, written , is the set of elements in B but not in A.
- When all sets under consideration are considered to be subsets of a given set U(Universal Set), the absolute complement of A is the set of elements in U but not in A.
 and
and  are any two sets.
are any two sets.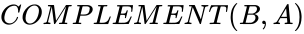 ,
, 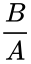 , is the set of elements in B but not in A.
, is the set of elements in B but not in A.