Difference between revisions of "Manuals/calci/MAKECOMPLEXIMINUSSIMPLE"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MAKECOMPLEXIMINUSSIMPLE(imaginary)'''</div><br/> *<math>imaginary</math> is the imaginary part of the complex number. ==Description== *MAKECO...") |
|||
| Line 18: | Line 18: | ||
*A Complex number whose real part is zero is said to be purely imaginary. | *A Complex number whose real part is zero is said to be purely imaginary. | ||
*A Complex number whose imaginary part is zero is a real number. In that cases we have to assign '0' for that part. | *A Complex number whose imaginary part is zero is a real number. In that cases we have to assign '0' for that part. | ||
| − | #=MAKECOMPLEXIMINUSSIMPLE (8) gives <math> | + | #=MAKECOMPLEXIMINUSSIMPLE (8) gives <math>0-i8</math> |
| − | #=MAKECOMPLEXIMINUSSIMPLE (2,["j"]) gives <math> | + | #=MAKECOMPLEXIMINUSSIMPLE (2,["j"]) gives <math>0-j2</math> |
==ZOS== | ==ZOS== | ||
| − | *The syntax is to calculate | + | *The syntax is to calculate MAKECOMPLEXIMINUSSIMPLE in ZOS is <math>MAKECOMPLEXIMINUSSIMPLE (IMAGINARY)</math> |
| − | <math>MAKECOMPLEXIMINUSSIMPLE (IMAGINARY)</math> | ||
*<math>IMAGINARY</math> is the imaginary part. | *<math>IMAGINARY</math> is the imaginary part. | ||
| Line 31: | Line 30: | ||
==Examples== | ==Examples== | ||
| − | #=MAKECOMPLEXIMINUSSIMPLE(5) = | + | #=MAKECOMPLEXIMINUSSIMPLE(5) = 0-i5 |
| − | #=MAKECOMPLEXIMINUSSIMPLE(-5 | + | #=MAKECOMPLEXIMINUSSIMPLE(-5) = 0+i5 |
| − | #=MAKECOMPLEXIMINUSSIMPLE(1) = | + | #=MAKECOMPLEXIMINUSSIMPLE(1) = 0-i1 |
| − | #=MAKECOMPLEXIMINUSSIMPLE( | + | #=MAKECOMPLEXIMINUSSIMPLE(-3,["j"]) = 0+j3 |
| Line 44: | Line 43: | ||
*[[Manuals/calci/COMPLEX | COMPLEX]] | *[[Manuals/calci/COMPLEX | COMPLEX]] | ||
| + | *[[Manuals/calci/MAKECOMPLEXIMINUS| MAKECOMPLEXIMINUS]] | ||
*[[Manuals/calci/MAKECOMPLEXISIMPLE| MAKECOMPLEXISIMPLE]] | *[[Manuals/calci/MAKECOMPLEXISIMPLE| MAKECOMPLEXISIMPLE]] | ||
*[[Manuals/calci/IMAGINARY | IMAGINARY]] | *[[Manuals/calci/IMAGINARY | IMAGINARY]] | ||
Revision as of 04:30, 17 April 2017
MAKECOMPLEXIMINUSSIMPLE(imaginary)
- is the imaginary part of the complex number.
Description
- MAKECOMPLEXIMINUSSIMPLE function represents a complex number using the imaginary coefficient mentioned in the argument. Here the imaginary coefficient is converted to negative value.
- As the argument does not contain real number, the real number coefficient is considered zero.
- A complex number is a combination of a real and an imaginary number.
- A number which is positive or negative, rational or irrational or decimals are called real numbers.
- An Imaginary number is a number that when squring it gives a negative result.
- For e.g. . Because a negative times a negative is positive.
- A complex number is in the form , where and are real numbers and is the imaginary unit. Where
- To mention and , we must use the lower case only
- In a complex number real part is denoted by & imaginary part is denoted by .
- MAKECOMPLEXIMINUSSIMPLE returns the error value, when and are non-numeric.
- should be either or , otherwise it shows error value.
- A Complex number whose real part is zero is said to be purely imaginary.
- A Complex number whose imaginary part is zero is a real number. In that cases we have to assign '0' for that part.
- =MAKECOMPLEXIMINUSSIMPLE (8) gives
- =MAKECOMPLEXIMINUSSIMPLE (2,["j"]) gives
ZOS
- The syntax is to calculate MAKECOMPLEXIMINUSSIMPLE in ZOS is
- is the imaginary part.
Examples
- =MAKECOMPLEXIMINUSSIMPLE(5) = 0-i5
- =MAKECOMPLEXIMINUSSIMPLE(-5) = 0+i5
- =MAKECOMPLEXIMINUSSIMPLE(1) = 0-i1
- =MAKECOMPLEXIMINUSSIMPLE(-3,["j"]) = 0+j3
Related Videos
See Also
References
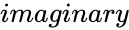 is the imaginary part of the complex number.
is the imaginary part of the complex number.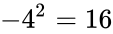 . Because a negative times a negative is positive.
. Because a negative times a negative is positive.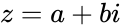 , where
, where  and
and  are real numbers and
are real numbers and  is the imaginary unit. Where
is the imaginary unit. Where 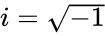
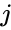 , we must use the lower case only
, we must use the lower case only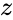 real part is denoted by
real part is denoted by 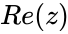 & imaginary part is denoted by
& imaginary part is denoted by 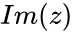 .
.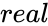 and
and 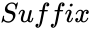 should be either
should be either 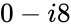
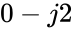
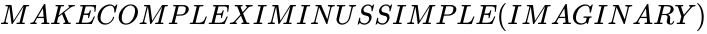
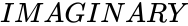 is the imaginary part.
is the imaginary part.