Difference between revisions of "Bartlett'sTest"
Jump to navigation
Jump to search
| Line 45: | Line 45: | ||
!8 | !8 | ||
|54 || 74 || 58 || 93 | |54 || 74 || 58 || 93 | ||
| + | |} | ||
| + | =BARTLETTSTEST(A1:A8,B1:B8,C1:C8,D1:D8,0.05,true) | ||
| + | {| class="wikitable" | ||
| + | |+BARTLETT'S TEST | ||
| + | |- | ||
| + | ! !!DATA-0!!DATA-1!! DATA-2!!DATA-3 | ||
| + | |- | ||
| + | |MEAN||60.375||77.875||78||71.875||0.22688||0.03081 | ||
| + | |- | ||
| + | |VARIANCE || 214.26785714285714 || 157.55357142857142 || 164.57142857142858 || 181.55357142857142 | ||
| + | |- | ||
| + | |LNVARIANCE || 5.367226901229239 || 5.059765536486956 || 5.1033446922005234 || 5.201550769540011 | ||
| + | |- | ||
| + | |COUNT || 8 || 8 || 8 || 8 | ||
| + | |- | ||
| + | |DF || 7 || 7 || 7 || 7 | ||
| + | |- | ||
| + | |1/DF || 0.14285714285714285 || 0.14285714285714285 || 0.14285714285714285 || 0.14285714285714285 | ||
|} | |} | ||
Revision as of 08:36, 9 May 2017
BARTLETTSTEST(DataRange,ConfidenceLevel,NewTableFlag)
- is the array of x values.
- is the value from 0 to 1.
- is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
Description
- Bartlett's test is used to test if k samples are from populations with equal variances.
- Bartlett's test is sensitive to departures from normality.
- That is, if the samples come from non-normal distributions, then Bartlett's test may simply be testing for non-normality.
- B is the Bartlett's test static.
- is the pooled variance across all groups.
Result
- If p-value is greater than BCriticl value, reject the null hypothesis.
- Else retain null hypothesis.
Example
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 51 | 82 | 79 | 85 |
| 2 | 87 | 91 | 84 | 80 |
| 3 | 50 | 92 | 74 | 65 |
| 4 | 48 | 80 | 98 | 71 |
| 5 | 79 | 52 | 63 | 67 |
| 6 | 61 | 79 | 83 | 51 |
| 7 | 53 | 73 | 85 | 63 |
| 8 | 54 | 74 | 58 | 93 |
=BARTLETTSTEST(A1:A8,B1:B8,C1:C8,D1:D8,0.05,true)
| DATA-0 | DATA-1 | DATA-2 | DATA-3 | |||
|---|---|---|---|---|---|---|
| MEAN | 60.375 | 77.875 | 78 | 71.875 | 0.22688 | 0.03081 |
| VARIANCE | 214.26785714285714 | 157.55357142857142 | 164.57142857142858 | 181.55357142857142 | ||
| LNVARIANCE | 5.367226901229239 | 5.059765536486956 | 5.1033446922005234 | 5.201550769540011 | ||
| COUNT | 8 | 8 | 8 | 8 | ||
| DF | 7 | 7 | 7 | 7 | ||
| 1/DF | 0.14285714285714285 | 0.14285714285714285 | 0.14285714285714285 | 0.14285714285714285 |
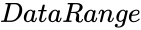 is the array of x values.
is the array of x values.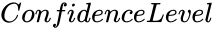 is the value from 0 to 1.
is the value from 0 to 1.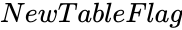 is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.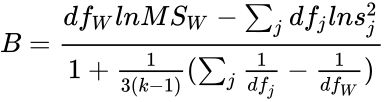
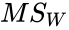 is the pooled variance across all groups.
is the pooled variance across all groups.