Difference between revisions of "Manuals/calci/MCORREL"
Jump to navigation
Jump to search
| Line 18: | Line 18: | ||
*Here x and y are viewed as the independent variables and z is the dependent variable. | *Here x and y are viewed as the independent variables and z is the dependent variable. | ||
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1.<math>Array of Arrays</math> are non-numeric or different number of data points. | + | 1.<math>Array of Arrays</math> are non-numeric or different number of data points. |
| − | 2.<math>Array of Arrays </math>is empty | + | 2.<math>Array of Arrays </math>is empty |
| − | 3.The denominator value is zero. | + | 3.The denominator value is zero. |
| + | |||
| + | ==Examples== | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/MATRIXMULTIPLY| MATRIXMULTIPLY]] | ||
| + | *[[Manuals/calci/MATRIXOPERATORS| MATRIXOPERATORS]] | ||
| + | *[[Manuals/calci/MATRIXMOD| MATRIXMOD ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://mtweb.mtsu.edu/stats/regression/level3/multicorrel/byhand.htm Multi Correl] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
==Examples== | ==Examples== | ||
Revision as of 17:02, 5 July 2017
MCORREL (ArrayOfArrays)
- is set of values.
Description
- This function is showing the result for multiple correlation.
- In , are set of values.
- Correlation is a statistical technique which shows the relation of strongly paired variables.When one variable is related to a number of other variables, the correlation is not simple.
- It is multiple if there is one variable on one side and a set of variables on the other side.
- If we have a series of measurements of and written as and where then the Sample Correlation Coefficient is:
- and are the sample means of and .
- The above formula is used for simple correlation.
- Now consider the variables x,y and z we define the multiple correlation as:
- is the correlation of x and y.
- is the correlation of y and z.
- is the correlation of z and x.
- Here x and y are viewed as the independent variables and z is the dependent variable.
- This function will give the result as error when
1. are non-numeric or different number of data points. 2.is empty 3.The denominator value is zero.
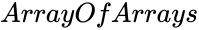 is set of values.
is set of values.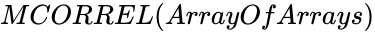 ,
,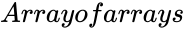 are set of values.
are set of values. measurements of
measurements of  and
and 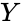 written as
written as 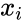 and
and 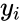 where
where 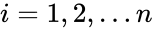 then the Sample Correlation Coefficient is:
then the Sample Correlation Coefficient is: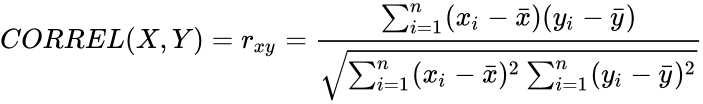
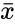 and
and 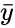 are the sample means of
are the sample means of 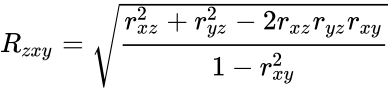
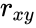 is the correlation of x and y.
is the correlation of x and y. is the correlation of y and z.
is the correlation of y and z. is the correlation of z and x.
is the correlation of z and x.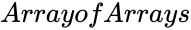 are non-numeric or different number of data points.
2.
are non-numeric or different number of data points.
2.