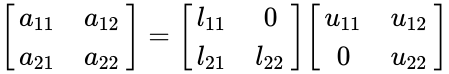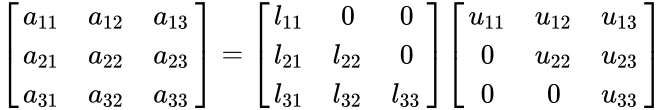Difference between revisions of "Manuals/calci/LUDECOMPOSITION"
Jump to navigation
Jump to search
| Line 17: | Line 17: | ||
l_{21}& l_{22} | l_{21}& l_{22} | ||
\end{bmatrix}\begin{bmatrix} | \end{bmatrix}\begin{bmatrix} | ||
| − | u_{ | + | u_{11} & u_{12} \\ |
0 & u_{22} | 0 & u_{22} | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
*For 3x3 matrix, | *For 3x3 matrix, | ||
| + | <math>\begin{bmatrix} | ||
| + | a_{11} & a_{12} & a_{13} \\ | ||
| + | a_{21}& a_{22} & a_{23}\\ | ||
| + | a_{31} & a_{32} & a_{33} | ||
| + | \end{bmatrix}=\begin{bmatrix} | ||
| + | l_{11} & 0 &0 \\ | ||
| + | l_{21}& l_{22} &0 \\ | ||
| + | l_{31}& l_{32} & l_{33} | ||
| + | \end{bmatrix}\begin{bmatrix} | ||
| + | u_{11} & u_{12} &u_{13} \\ | ||
| + | 0 & u_{22} &u_{23} \\ | ||
| + | 0 & 0 & u_{33} | ||
| + | \end{bmatrix}</math> | ||
Revision as of 17:23, 11 July 2017
LUDECOMPOSITION (Matrix)
- is the set of values.
Description
- This function gives the value of LU Decomposition of a given matrix.
- In , is any square matrix.
- LU Decomposition is the procedure for decomposing any square matrix in to a product of Lower Triangular matrix and Upper Triangular matrix.
- In LU Decomposition,L stands for Lower Triangular matrix and U stands for Upper Triangular matrix.
- So A=LU.But sometimes the product includes Permutation Matrix also.
- LU Decomposition is also called LU Factorization.Here given matrix is split in to lower triangular and Upper triangular matrix.
- For 2x2 matrix,
- For 3x3 matrix,
 is the set of values.
is the set of values. ,
,