Difference between revisions of "Manuals/calci/GOLDENRATIO"
Jump to navigation
Jump to search
| Line 14: | Line 14: | ||
*Using quadratic formula, golden ratio is represented as - | *Using quadratic formula, golden ratio is represented as - | ||
| − | <math>\phi</math> | + | <math>\phi</math> = <math>\frac{(1 + \sqrt 5)}{2}</math> = 1.618033988749895 |
| − | <math>\Phi</math> | + | <math>\Phi</math> = <math>\frac{(1 - \sqrt 5)}{2}</math> = -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi) |
*Argument <math>phismall</math> can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1. | *Argument <math>phismall</math> can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1. | ||
Revision as of 16:08, 20 July 2017
GOLDENRATIO(phismall)
- where is the logical value TRUE or FALSE.
GOLDENRATIO() returns the golden ratio value.
Description
- Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities.
- Golden ratio is represented as φ(phi or smallphi) and its conjugate is represented as Φ(Phi or capitalphi).
- If 'a' and 'b' are two quantities with 'a>b', then
φ = =
- Using quadratic formula, golden ratio is represented as -
= = 1.618033988749895
= = -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi)
- Argument can be logical values TRUE (or 1) or FALSE (or 0). Any other argument values are ignored and Calci assumes it to be TRUE or 1.
- If argument is omitted, Calci assumes it as TRUE or 1 and displays the output as 0.6180339887498948.
- If argument is invalid, Calci returns a #NULL error message.
Examples
GOLDENRATIO(TRUE) returns 0.6180339887498948, value of capitalphi Φ
GOLDENRATIO(1) returns 0.6180339887498948, value of capitalphi Φ
GOLDENRATIO(FALSE) returns 1.618033988749895, value of smallphi φ
GOLDENRATIO() returns 0.6180339887498948, value of capitalphi Φ
Related Videos
See Also
References
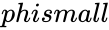 is the logical value TRUE or FALSE.
is the logical value TRUE or FALSE.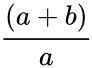 =
= 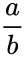
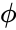 =
=  = 1.618033988749895
= 1.618033988749895
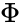 =
=  = -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi)
= -0.6180339887498948 (Absolute value 0.6180339887498948 is considered as capitalphi)