Difference between revisions of "Manuals/calci/LISSAJOUSCURVE"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''LISSAJOUSCURVE()'''</div><br/> ==Description== *This function shows the Lissajous curve for each values. *Lissajous Curve is a parametric plo...") |
|||
| Line 8: | Line 8: | ||
*A beam of light reflected from the mirror, was allowed to trace patterns which depended on the frequencies of the sounds – in a setup similar to projectors used in today's laser light shows. | *A beam of light reflected from the mirror, was allowed to trace patterns which depended on the frequencies of the sounds – in a setup similar to projectors used in today's laser light shows. | ||
*Lissajous figure is the intersection of two sinusoidal curves, the axes of which are at right angles to each other. | *Lissajous figure is the intersection of two sinusoidal curves, the axes of which are at right angles to each other. | ||
| − | *Mathematically, this translates to a Complex harmonic function:The appearance of a figure is highly sensitive to a/b, the ratio of a and b. | + | *Mathematically, this translates to a Complex harmonic function: |
| + | <math>x=A Sin(at+\delta)</math>,<math>y=B Sin(bt)</math> | ||
| + | *The appearance of a figure is highly sensitive to a/b, the ratio of a and b. | ||
*According to the ratio value, the shapes of the figures change in interesting ways. | *According to the ratio value, the shapes of the figures change in interesting ways. | ||
*For a a/b ratio=1, the figure is an ellipse. | *For a a/b ratio=1, the figure is an ellipse. | ||
Revision as of 16:36, 23 August 2017
LISSAJOUSCURVE()
Description
- This function shows the Lissajous curve for each values.
- Lissajous Curve is a parametric plot of the harmonic system.
- It is also called Bowditch Curves.Lissajous used sounds of different frequencies to vibrate a mirror.
- A beam of light reflected from the mirror, was allowed to trace patterns which depended on the frequencies of the sounds – in a setup similar to projectors used in today's laser light shows.
- Lissajous figure is the intersection of two sinusoidal curves, the axes of which are at right angles to each other.
- Mathematically, this translates to a Complex harmonic function:
,
- The appearance of a figure is highly sensitive to a/b, the ratio of a and b.
- According to the ratio value, the shapes of the figures change in interesting ways.
- For a a/b ratio=1, the figure is an ellipse.
- For a=b, = radians, the figure is a circle.
- For = 0, the figure is a line.
- For a/b = 2, = , the result is a parabola.
- The Lissajous curve gets more complicated for other ratios, which are closed only if a/b is rational.
Examples
See Also
References
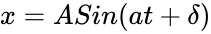 ,
,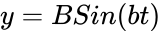
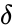 =
= 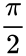 radians, the figure is a circle.
radians, the figure is a circle.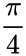 , the result is a parabola.
, the result is a parabola.