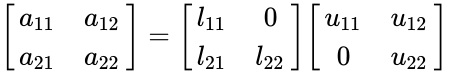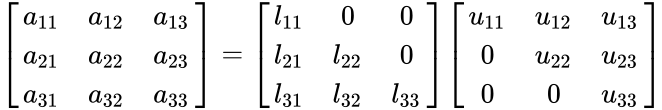Difference between revisions of "Manuals/calci/LUDECOMPOSITION"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*In <math>LUDECOMPOSITION (Matrix)</math>, <math>Matrix</math> is any square matrix. | *In <math>LUDECOMPOSITION (Matrix)</math>, <math>Matrix</math> is any square matrix. | ||
*LU Decomposition is the procedure for decomposing any square matrix in to a product of Lower Triangular matrix and Upper Triangular matrix. | *LU Decomposition is the procedure for decomposing any square matrix in to a product of Lower Triangular matrix and Upper Triangular matrix. | ||
| − | *In LU Decomposition,L stands for Lower Triangular matrix and U stands for Upper Triangular matrix. | + | *In LU Decomposition, L stands for Lower Triangular matrix and U stands for Upper Triangular matrix. |
*So A=LU.But sometimes the product includes Permutation Matrix also. | *So A=LU.But sometimes the product includes Permutation Matrix also. | ||
*LU Decomposition is also called LU Factorization.Here given matrix is split in to lower triangular and Upper triangular matrix. | *LU Decomposition is also called LU Factorization.Here given matrix is split in to lower triangular and Upper triangular matrix. | ||
Revision as of 06:59, 4 September 2017
LUDECOMPOSITION (Matrix)
- is the set of values.
Description
- This function gives the value of LU Decomposition of a given matrix.
- In , is any square matrix.
- LU Decomposition is the procedure for decomposing any square matrix in to a product of Lower Triangular matrix and Upper Triangular matrix.
- In LU Decomposition, L stands for Lower Triangular matrix and U stands for Upper Triangular matrix.
- So A=LU.But sometimes the product includes Permutation Matrix also.
- LU Decomposition is also called LU Factorization.Here given matrix is split in to lower triangular and Upper triangular matrix.
- For 2x2 matrix,
- For 3x3 matrix,
Examples
1. LUDECOMPOSITION([4,3;6,3])
|
1 0 |
0.6666666666666666 1 |
|
6 3 |
0 1 |
|
0 1 |
1 0 |
2. LUDECOMPOSITION([[10,12,16],[-8,-4,15],[20,24,28]])
|
1 0 0 |
-0.4 1 0 | 0.5 0 1 |
|
20 24 28 |
0 5.600000000000001 26.200000000000003 |
0 0 2 |
|
0 0 1 |
0 1 0 |
1 0 0 |
 is the set of values.
is the set of values. ,
,