Difference between revisions of "Manuals/calci/SVD"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*Singular value decomposition is defined for all matrices (rectangular or square). | *Singular value decomposition is defined for all matrices (rectangular or square). | ||
| − | Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers. | + | Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers. |
*Then there exists a factorization, called a singular value decomposition of A, of the form | *Then there exists a factorization, called a singular value decomposition of A, of the form | ||
where | where | ||
| − | |||
U is an m × m unitary matrix, | U is an m × m unitary matrix, | ||
S is a diagonal m × n matrix with non-negative real numbers on the diagonal, | S is a diagonal m × n matrix with non-negative real numbers on the diagonal, | ||
V is an n × n unitary matrix over K, and | V is an n × n unitary matrix over K, and | ||
<math>V^T</math> is the conjugate transpose of V. | <math>V^T</math> is the conjugate transpose of V. | ||
Revision as of 08:47, 4 September 2017
SVD(Matrix)
- is the set of values.
Description
- The singular value decomposition of a matrix A is the factorization of A into the product of three matrices
- Where the columns of U and V are orthonormal and the matrix S is diagonal with positive real entries
- Singular value decomposition is defined for all matrices (rectangular or square).
Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers.
- Then there exists a factorization, called a singular value decomposition of A, of the form
where U is an m × m unitary matrix, S is a diagonal m × n matrix with non-negative real numbers on the diagonal, V is an n × n unitary matrix over K, and is the conjugate transpose of V.
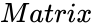 is the set of values.
is the set of values.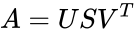
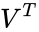 is the conjugate transpose of V.
is the conjugate transpose of V.