Difference between revisions of "Manuals/calci/QUATERNION"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*Quartenion is a complex number of the form w + xi + yj + zk, where w, x, y, z are real numbers and i, j, k are imaginary units. | *Quartenion is a complex number of the form w + xi + yj + zk, where w, x, y, z are real numbers and i, j, k are imaginary units. | ||
*The imaginary units are satisfy certain conditions: | *The imaginary units are satisfy certain conditions: | ||
| − | *<math>i^{2}=j^2=k^2=ijk= -1</math>. | + | * <math>i^{2}=j^2=k^2=ijk= -1</math>. |
| − | *<math>i\sdot j =k= −j*i</math>,<math>j*k = i = −k*j</math>, <math>k*i = j = −i*k</math> | + | *<math>i\sdot j </math> =<math>k</math>= −j*i</math>,<math>j*k = i = −k*j</math>, <math>k*i = j = −i*k</math> |
==Examples== | ==Examples== | ||
Revision as of 13:36, 17 January 2018
QUATERNION (a,b,c,d)
- and are any real numbers.
Description
- This function shows the coefficient of the Quarternion.
- In , and are any real numbers.
- Quartenion is a complex number of the form w + xi + yj + zk, where w, x, y, z are real numbers and i, j, k are imaginary units.
- The imaginary units are satisfy certain conditions:
- .
- == −j*i</math>,Failed to parse (syntax error): {\displaystyle j*k = i = −k*j} , Failed to parse (syntax error): {\displaystyle k*i = j = −i*k}
Examples
- QUATERNION(9,2,3,4) = 9 2 3 4
- QUATERNION(8,-2,4,-5) = 8 -2 4 -5
- QUATERNION(-9,-12,-16,-20) = -9 -12 -16 -20
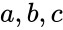 and
and 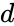 are any real numbers.
are any real numbers.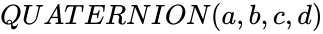 ,
,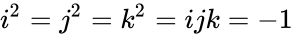 .
.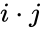 =
=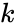 = −j*i</math>,Failed to parse (syntax error): {\displaystyle j*k = i = −k*j}
, Failed to parse (syntax error): {\displaystyle k*i = j = −i*k}
= −j*i</math>,Failed to parse (syntax error): {\displaystyle j*k = i = −k*j}
, Failed to parse (syntax error): {\displaystyle k*i = j = −i*k}