Difference between revisions of "Manuals/calci/ERF"
Jump to navigation
Jump to search
| Line 2: | Line 2: | ||
*<math>a</math> is the lower limit and <math> b </math> is the upper limit. | *<math>a</math> is the lower limit and <math> b </math> is the upper limit. | ||
*<math>accuracy</math> gives accurate value of the solution | *<math>accuracy</math> gives accurate value of the solution | ||
| + | **ERF(), returns the Error Function. | ||
==Description== | ==Description== | ||
Revision as of 17:15, 13 July 2018
ERF(a,b,accuracy)
- is the lower limit and is the upper limit.
- gives accurate value of the solution
- ERF(), returns the Error Function.
Description
- This function gives the value of the error function .
- Error function is the special function which is encountered in integrating the normal distribution.
- In , is the lower limit of the integrating function and is the upper limit of the integrating function.
- Also is optional. When we are omitting the value, then the integral of the error function between 0 and the given value is returned otherwise it will consider the given and values.
- This function is also called Gauss error function.
- is defined by:
- .
- In this case is the lower limit and is the upper limit.
- This function will return the result as error when
1.any one of the argument is non-numeric. 2. or is negative.
ZOS
- The syntax is to calculate error function in ZOS is .
- is the lower limit and is the upper limit.
- gives accurate value of the solution.
- For e.g.,erf(2,3),erf(2,3,0.001)
Examples
- ERF(1,2)=0.15262153
- ERF(3,2)=-0.004655645
- ERF(0,1)=0.842700735
- ERF(5)=1.0000001892118586
- ERF(-3)=NAN
Related Videos
See Also
References
 is the lower limit and
is the lower limit and  is the upper limit.
is the upper limit.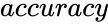 gives accurate value of the solution
gives accurate value of the solution
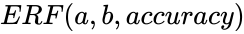 ,
, is defined by:
is defined by: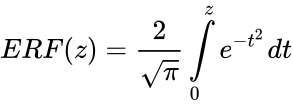
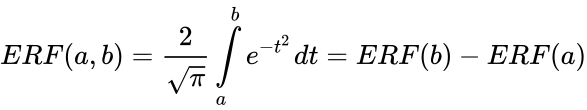 .
.