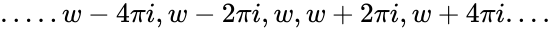Difference between revisions of "Manuals/calci/IMLOG"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''IMLOG (ComplexNumber,Base)'''</div><br/> | <div style="font-size:30px">'''IMLOG (ComplexNumber,Base)'''</div><br/> | ||
| − | *<math>ComplexNumber</math> is any complex number. | + | *<math>ComplexNumber</math> is any complex number of the form x+iy. |
*<math>Base</math> is the base value of the Log. | *<math>Base</math> is the base value of the Log. | ||
**IMLOG(),returns the logarithm of a complex number to the given base. | **IMLOG(),returns the logarithm of a complex number to the given base. | ||
Revision as of 15:42, 19 July 2018
IMLOG (ComplexNumber,Base)
- is any complex number of the form x+iy.
- is the base value of the Log.
- IMLOG(),returns the logarithm of a complex number to the given base.
Description
- This function shows the log value of a complex number.
- In , is any complex number.
- is the base value of a Log values.
- A complex logarithm function is an "inverse" of the complex exponential function.
- It is same as the real natural logarithm ln x is the inverse of the real exponential function.
- Thus, a logarithm of a complex number z is a complex number w such that .
- The notation for such a is or .
- If with which is in Polar form, then is one logarithm of z.
- Adding integer multiples of 2πi gives all the others.
- The complex exponential function is not injective, because for any w, since adding iθ to w has the effect of rotating counterclockwise θ radians.
- So the points
Examples
- IMLOG("2+3i",2) = 1.850219859070546+ⅈ1.417871630745722
- IMLOG("9-5i",3) = 2.122422597222964-ⅈ0.4615809504617068
- IMLOG("9-5i",6) = 1.3013574573492332-ⅈ0.2830170640096076
- IMLOG("54",5) =2.4784951415313494+ⅈ0
- IMLOG("-19i",9) = 1.3400719296231876-ⅈ0.7149002168450317
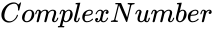 is any complex number of the form x+iy.
is any complex number of the form x+iy.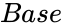 is the base value of the Log.
is the base value of the Log.
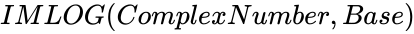 ,
,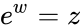 .
.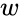 is
is 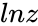 or
or 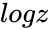 .
.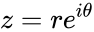 with
with 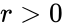 which is in Polar form, then
which is in Polar form, then 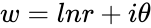 is one logarithm of z.
is one logarithm of z.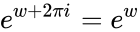 for any w, since adding iθ to w has the effect of rotating
for any w, since adding iθ to w has the effect of rotating 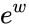 counterclockwise θ radians.
counterclockwise θ radians.