ERF(ll,ul)
- is the lower limit and is the upper limit.
Description
- This function gives the value of the error function .
- Error function is the special function which is encountered in integrating the normal distribution.
- In is the lower limit of the integrating function and is the upper limit of the integrating function.
- Also is optional. When we are omitting the value, then the integral of the error function between 0 and the given value is returned otherwise it will consider the given and values.
- This function is also called Gauss error function. is defined by:
Failed to parse (syntax error): {\displaystyle ERF(a,b)=\frac{2}{\sqrt{\pi}\int\limits_{a}^{b}e^{-t^2} dt=ERF(b)-ERF(a)} .
- In this case 'a' is the lower limit and 'b' is the upper limit.
- This function will return the result as error when
- any one of the argument is nonnumeric.
- ll or ul is negative.
Examples
- ERF(1,2)=0.15262153
- ERF(3,2)=-0.004655645
- ERF(0,1)=0.842700735
- ERF(5)=1
- ERF(-3)=NAN
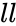 is the lower limit and
is the lower limit and 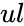 is the upper limit.
is the upper limit.