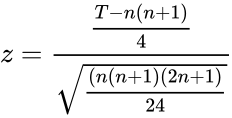Manuals/calci/WILCOXONSIGNEDRANKTEST
- is the array of x values.
- is the array of y values.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the summary values of Wilcoxon signed rank test.
- This test is the one of the Non Parametric test.
- Nonparametric test is also called Distribution Free Test.
- So Wilcoxon Rank test is not depending on the parameters.
- This test is designed to test a hypothesis about the median of a population distribution.
- It often involves the use of matched pairs, for example, before and after data, in which case it tests for a median difference of zero.
- Also this test does not require the assumption that the population is normally distributed.
- This test is the alternative of the Student's T-test.
- Normally this test is the version of the dependent samples t-test that can be performed on the ranked data.
- i.e., When the requirements for the t-test for two paired samples are not satisfied, the Wilcoxon Signed-Rank Test for Paired Samples non-parametric test can often be used.
- It is a more powerful alternative to the sign test, but does assume that the population probability distribution is symmetric.
- For this test let us consider the n subjects from the population with two observations and .
- The requirements for the Wilcoxon Signed-Rank Tests for Paired Samples where Failed to parse (syntax error): {\displaystyle z_i = y_i–x_i} for all i = 1, … ,n, are as follows:
1.the are independent. 2. and are interval data.
- This test containing the following steps:
- 1.Define Null and Alternative hypothesis:
- Null hypothesis = There is no difference between the two observations.
- Alternative hypothesis = There is a difference between the two observations.
- 2.State alpha(Confidence level): alpha value is from 0 to 1.
- 3.State Decision Rule: Fix the hypothesis value according to the z table.
- 4.Calculate Test Statistic:
where T is the smallest rank value and n is the number of observations.
- 5.State Result: In this step we have to take a decision of null hypothesis either accept or reject depending on the z value.
- 6.State Conclusion: How far the value of the test before and after the grouping.
- The Wilcoxon signed Rank test result is contains the following values in the table:Difference of the ach observation, Absolute value of the difference,Rank value,Signed Rank and the test value.
Examples
WILCOXON SIGNED RANK TEST FOR PAIRED SAMPLES
| X1 | X2 |
| 188 | 186 |
| 177 | 171 |
| 176 | 177 |
| 169 | 168 |
| 196 | 191 |
| 172 | 172 |
| 165 | 177 |
| 190 | 191 |
| 165 | 170 |
| 180 | 171 |
| 181 | 188 |
| 172 | 187 |
- =WILCOXONSIGNEDRANKTEST(A1:A12,B1:B12,0.05,2,TRUE) [For Two Tailed Test]
or
- =WILCOXONSIGNEDRANKTEST(A1:A12,B1:B12,0.05,1,TRUE) [For One Tailed Test]
| X1 | X2 | Abs(Diff) | Sign | Rank | SignedRank |
|---|---|---|---|---|---|
| 188 | 186 | 2 | -1 | 4 | -4 |
| 177 | 171 | 6 | -1 | 7 | -7 |
| 176 | 177 | 1 | 1 | 2 | 2 |
| 169 | 168 | 1 | -1 | 2 | -2 |
| 196 | 191 | 5 | -1 | 5.5 | -5.5 |
| 172 | 172 | 0 | 0 | 0 | 0 |
| 165 | 177 | 12 | 1 | 10 | 10 |
| 190 | 191 | 1 | 1 | 2 | 2 |
| 165 | 170 | 5 | 1 | 5.5 | 5.5 |
| 180 | 171 | 9 | -1 | 9 | -9 |
| 181 | 188 | 7 | 1 | 8 | 8 |
| 172 | 187 | 15 | 1 | 11 | 11 |
| N | Mean Rank | SUM of Ranks | |
|---|---|---|---|
| Negative Ranks | 5 | -5.5 | -27.5 |
| Positive Ranks | 6 | 6.416666666666667 | 38.5 |
| Nr | 11 |
| W | 11 |
| Standard Deviation | 22.4944 |
| Mean | 33 |
| Z-value | 0.489 |
| p-value(Two Tail) | 0.6248 |
WILCOXON SIGNED RANK TEST FOR MEDIAN (SINGLE SAMPLE)
| X |
| -2 |
| -3 |
| 8 |
| 4 |
| 6 |
| -4 |
| -11 |
| -2 |
| -12 |
| -6 |
- MEDIAN = 0
- =WILCOXONSIGNEDRANKTEST(A1:A9,0,0.05,2,TRUE) [For Two Tailed Test]
or
- =WILCOXONSIGNEDRANKTEST(A1:A9,0,0.05,1,TRUE) [For One Tailed Test]
| X1 | X2 | Abs(Diff) | Sign | Rank | SignedRank |
|---|---|---|---|---|---|
| -2 | _ | 2 | 1 | 1.5 | 1.5 |
| -3 | _ | 3 | 1 | 3 | 3 |
| 8 | _ | 8 | -1 | 8 | -8 |
| 4 | _ | 4 | -1 | 4.5 | -4.5 |
| 6 | _ | 6 | -1 | 6.5 | -6.5 |
| -4 | _ | 4 | 1 | 4.5 | 4.5 |
| -11 | _ | 11 | 1 | 9 | 9 |
| -2 | _ | 2 | 1 | 1.5 | 1.5 |
| -12 | _ | 12 | 1 | 10 | 10 |
| -6 | _ | 6 | 1 | 6.5 | 6.5 |
| N | Mean Rank | SUM of Ranks | |
|---|---|---|---|
| Negative Ranks | 3 | -6.333333333333333 | -19 |
| Positive Ranks | 7 | 5.142857142857143 | 36 |
| Nr | 10 |
| W | 17 |
| Standard Deviation | 19.6214 |
| Mean | 27.5 |
| Z-value | 0.8664 |
| p-value(Two Tail) | 0.3863 |
WILCOXON SIGNED RANK TEST FOR SMALL SAMPLES
The lower and upper critical values,W, of the Wilcoxon Signed Rank test can be found from the table for samples size less than 10.
For a two-tail test, you reject the null hypothesis, if the computed W test statistic equals or is greater than the upper critical value or is equal to or less than the lower critical value.
For a one-tail test in the lower tail, you reject the null hypothesis if the computed W test statistic is less than or equal to the lower critical value.
For a onetail test in the upper tail, the decision rule is to reject the null hypothesis if the computed W test statistic equals or is greater than the upper critical value
| X1 | X2 |
| 85 | 75 |
| 70 | 50 |
| 40 | 50 |
| 65 | 40 |
| 80 | 20 |
| 75 | 65 |
| 55 | 40 |
| 20 | 25 |
- =WILCOXONSIGNEDRANKTEST(A1:A9,B1:B9,0.05,2,TRUE) [For Two Tailed Test]
or
- =WILCOXONSIGNEDRANKTEST(A1:A9,B1:B9,0.05,1,TRUE) [For One Tailed Test]
| X1 | X2 | Abs(Diff) | Sign | Rank | SignedRank |
|---|---|---|---|---|---|
| 85 | 75 | 10 | -1 | 3 | -3 |
| 70 | 50 | 20 | -1 | 6 | -6 |
| 40 | 50 | 10 | 1 | 3 | 3 |
| 65 | 40 | 25 | -1 | 7 | -7 |
| 80 | 20 | 60 | -1 | 8 | -8 |
| 75 | 65 | 10 | -1 | 3 | -3 |
| 55 | 40 | 15 | -1 | 5 | -5 |
| 20 | 25 | 5 | 1 | 1 | 1 |
| N | Mean Rank | SUM of Ranks | |
|---|---|---|---|
| Negative Ranks | 6 | -5.333333333333333 | -32 |
| Positive Ranks | 2 | 2 | 4 |
| Nr | 8 |
| W-Calculated | -28 |
| W-LowerTail | 5 |
| W-UpperTail | 31 |
| Standard Deviation | 14.2829 |
| Mean | 18 |
| Z-value | -1.9604 |
| p-value(Two Tail) | 0.05 |
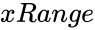 is the array of x values.
is the array of x values.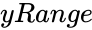 is the array of y values.
is the array of y values.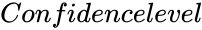 is the value between 0 and 1.
is the value between 0 and 1.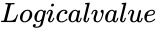 is either TRUE or FALSE.
is either TRUE or FALSE.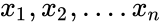 and
and 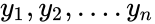 .
.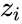 are independent.
2.
are independent.
2.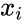 and
and 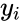 are interval data.
are interval data.
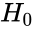 = There is no difference between the two observations.
= There is no difference between the two observations.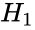 = There is a difference between the two observations.
= There is a difference between the two observations.