Manuals/calci/IMSQRT
Jump to navigation
Jump to search
IMSQRT(z)
- is the complex number is of the form
Description
- This function gives square root of a complex number.
- IMSQRT(z), Where z is the complex number is in the form of "x+iy".
- where x&y are the real numbers.'i' imaginary unit.
- The square root of a complex number is defined by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt(z)=\sqrt{x+iy}=\sqrt{r.e^iθ}=sqrt(r)[cos(θ/2)+isin(θ/2)],where r is the modulus of z.<math>r=\sqrt(x^2+y^2)} and θ is the argument of z.Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle θ=tan^-1(y/x)} also θ∈(-Pi(),Pi()].
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Remarks
Examples
''''''' ''''
Description
This function calculates the square root of a complex number in a + bi or a + bj text format.
IMSQRT
The square root of a complex number is:
IMSQRT(IN)
where IN is the complex number
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 1.455346690225355+0.34356074972251243i | |||
| Row2 | ||||
| Row3 | ||||
| Row4 | ||||
| Row5 | ||||
| Row6 |
Let's see an example
I.e =IMSQRT(“2+i”) is 1.4553+0.34356i
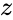 is the complex number is of the form
is the complex number is of the form 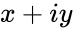
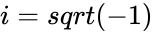 .
.