Manuals/calci/INQUADRANTSIGN
INQUADRANTSIGN (Quadrant,TrigFunction)
- is the quadrant number.
- is any trigonometric function.
Description
- This function shows the sign of the trigonometric functions in each quadrant.
- In , is the quadrant number.
- is the trigonometric function.
- Generally there are Four quadrants.
- Quadrants are defined by the axes of a two dimensional Cartesian system divide the plane into four infinite regions and each bounded by two half-axes.
- The sign of a trigonometric function is dependent on the signs of the coordinates of the points on the terminal side of the angle.
- By knowing in which quadrant the terminal side of an angle lies, you also know the signs of all the trigonometric functions.
- There are eight regions in which the terminal side of an angle may lie: in any of the four quadrants, or along the axes in either the positive or negative direction.
- The distance from a point to the origin is always positive, but the signs of the x and y coordinates may be positive or negative.
- Thus, in the first quadrant, where x and y coordinates are all positive, all six trigonometric functions have positive values.
- In the second quadrant, only sine and cosecant (the reciprocal of sine) are positive.
- In the third quadrant, only tangent and cotangent are positive.
- Finally, in the fourth quadrant, only cosine and secant are positive.
Examples
- INQUADRANTSIGN(1,"SIN") = 1
- INQUADRANTSIGN(2,"TAN") = -1
- INQUADRANTSIGN(4,"COS") = 1
See Also
References
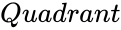 is the quadrant number.
is the quadrant number.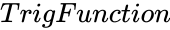 is any trigonometric function.
is any trigonometric function.