Manuals/calci/IMDIV
Jump to navigation
Jump to search
IMDIV(z1,z2)
- are the two complex numbers in the form of and , where Failed to parse (syntax error): {\displaystyle a,b,c<math> & <math>d<math> are real numbers <math>i} is the imaginary unit, <math>i=\sqrt{-1}<math>.
- To do the division of complex number we have follow the steps:
step 1: We have to write the complex number is in the fraction form. step 2: To find the conjugate of the denominator. step 3: To mutiply the numerator and denominator with conjugate.
i.e. <math>IMDIV(z1,z2) = \frac{a+ib}{c+id} = \frac{a+ib}{c+id}*\frac{c-id}{c-id} =\frac{ac+bd}{c^2+d^2}+\frac{(bc-ad)i}{(c^2+d^2)}
Examples
- IMDIV("4+2i","3-i")=(4+2i/3-i)*(3+i/3+i)=(12+10i+2i^2)/(3^2-i^2)=10+10i/10 (because i^2=-1)= 1+i/1=1+i
- IMDIV("3-5i,2-6i")=0.9+0.2i
- IMDIV("5","2+3i")=0.769-1.153i
- IMDIV("1+i","2")=0.5+0.5i
See Also
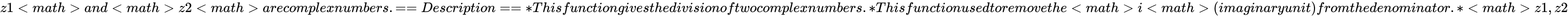 are the two complex numbers in the form of
are the two complex numbers in the form of  and
and 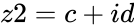 , where Failed to parse (syntax error): {\displaystyle a,b,c<math> & <math>d<math> are real numbers <math>i}
is the imaginary unit, <math>i=\sqrt{-1}<math>.
, where Failed to parse (syntax error): {\displaystyle a,b,c<math> & <math>d<math> are real numbers <math>i}
is the imaginary unit, <math>i=\sqrt{-1}<math>.