Manuals/calci/SKEW
Jump to navigation
Jump to search
SKEW(n1,n2,…)
- are numbers to calculate the skewness.
Description
- This function gives the Skewness of a distribution.
- Skewness is a measure of the degree of asymmetry of a distribution.
- A distribution(normal distribution) is symmetry ,it don't have a Skewness.
- In a distribution the left tail is more pronounced than the right tail (towards more negative values) then the function is said to have Negative Skewness.
- If a distribution is skewed to the right, the tail on the curve's right-hand side is longer than the tail on the left-hand side (towards more positive values), then the function is said to have a positive skewness.
- In a Left Skewed Distribution, its
- In a Normal Skewed Distribution, its
- In a Right Skewed Distribution, its .
- In is required. are optional.
- In calci there is no restriction for giving the number of arguments.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logicl values or empty cells, like that values are not considered.
- The equation for Skewness is defined by :
Where, is the sample standard deviation, represents a sample mean.
- This function will return the result as error when
1. Any one of the argument is non-numeric. 2. If there are fewer than three data points, or the Sample Standard Deviation is zero.
Examples
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 0 | 4 | -5 | 4 | 1 |
| 2 | 29 | 9 | 11 | 5 | 2 |
| 3 | 41 | 11 | 18 | 2 | 3 |
| 4 | 18 | 10 | 7 | 5 | 5 |
| 5 | 4 | 5 | 9 | 6 | 6 |
| 6 | 38 | 9 | 13 | 8 | 11 |
- =SKEW(B1:B5) = -0.4369344921493
- =SKEW(A1:A6) = -0.21921252920
- =SKEW(C1:C4) = -0.715957010
- =SKEW(D1:D6) = 0
- =SKEW(E1:E6) = 1.16584702768
Related Videos
See Also
References
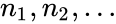 are numbers to calculate the skewness.
are numbers to calculate the skewness.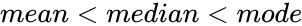
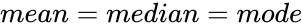
 .
.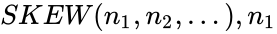 is required.
is required.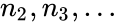 are optional.
are optional.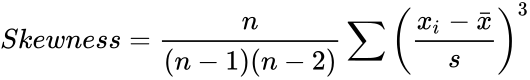
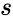 is the sample standard deviation,
is the sample standard deviation, 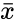 represents a sample mean.
represents a sample mean.