Manuals/calci/IMDIV
IMDIV(z1,z2)
- and are complex numbers.
Description
- This function gives the division of two complex numbers.
- This function used to remove the (imaginary unit) from the denominator.
- are the two complex numbers in the form of and , where & are real numbers is the imaginary unit, .
- To do the division of complex number we have follow the steps:
step 1: We have to write the complex number is in the fraction form. step 2: To find the conjugate of the denominator. step 3: To mutiply the numerator and denominator with conjugate.
i.e.
Examples
- IMDIV("4+2i","3-i") = (4+2i/3-i)*(3+i/3+i) = (12+10i+2i^2)/(3^2-i^2) = 10+10i/10 (because ) = 1+i/1 = 1+i
- IMDIV("3-5i,2-6i")=0.9+0.2i
- IMDIV("5","2+3i")=0.769-1.153i
- IMDIV("1+i","2")=0.5+0.5i
See Also
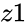 and
and 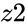 are complex numbers.
are complex numbers.