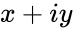IMLOG2(z)
- is the complex number is of the form
Description
- This function gives the binary logarithm of a complex number.
- IMLOG2(z),Where z is the complex number in the form of "x+iy".i.e. x&y are the real numbers.
- 'I' imaginary unit .i=sqrt(-1).
- Binary logarithm is the inverse function of n ↦ 2n.
- Log base 2 is called Binary logarithm.
- To find the Binary logarithm of a complex number we have to calculate from the natural logarithm.
- So log2(x+iy)=(log2 e)ln(x+iy).We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMLOG2("2+3i")=1.85021985921295+1.41787163085485i
- IMLOG2("5-6i")=2.96536866900967-1.26388460522614i
- IMLOG2("15")=3.90689059590921
- IMLOG2("11i")=3.45943161890355+2.26618007108801i
- IMLOG2("0")=NULL
See Also
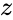 is the complex number is of the form
is the complex number is of the form