Manuals/calci/IMPOWER
IMPOWER(z,n)
- is the complex number is of the form
- is the power value.
Description
- This function gives the value of powers of complex number.
- DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form.
- i'is the imaginary unit,
- Then the power of a complex number is defined by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (z)^n=(x+iy)^n=r^n*e^{inθ}=r^n(cosnθ+isinnθ)} where . and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle θ=tan^-1(y/x)} , θ∈(-Pi(),Pi()].
- This formula is called DeMoivre's theorem of complex numbers.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
- In IMPOWER(z,n), n can be integer, fractional or negative.
- suppose n is nonnumeric , this function will returns the error value.
Examples
- IMPOWER("4+5i",3)=-235.99999+115i
- IMPOWER("9-7i",4)=-14852-8063.999999i
- IMPOWER("6",9)=10077696
- IMPOWER("i",10)=-1+6.1257422745431E-16i
See Also
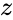 is the complex number is of the form
is the complex number is of the form 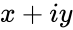
 is the power value.
is the power value.