LOGNORMDIST((x,m,sd)
- is the value , is the mean of ,
- And is the standard deviation of .
Description
- This function gives the value of the cumulative log normal distribution.
- This distribution is the continuous probability distribution.
- Lognomal distribution is also called Galton's distribution.
- A random variable which is log-normally distributed takes only positive real values.
- Suppose is normally distributed function ,then also normally distributed
- also normally distributed.
- Let the normal distribution function and its mean= Failed to parse (syntax error): {\displaystyle μ} , standard deviation = Failed to parse (syntax error): {\displaystyle σ}
- Then the lognormal cumulative distribution is calculated by:Failed to parse (syntax error): {\displaystyle F(x,μ,σ)=1/2[1+(erf(ln(x)-μ)/σsqrt(2)= φ[(ln(x)-μ)/σ]} where erf is the error function( the error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations)
- And φ is the cumulative distribution function of the standard normal distribution.
- This function will give the result as error when
1. Any one of the argument is nonnumeric. 2.suppose or
It calculates the cumulative lognormal distribution of x, where ln(x) is distributed with parameters as mean and standard deviation.
· When arguments are nonnumeric ,LOGNORMDIST shows error.
· LOGNORMDIST displays 0, when n ≤ 0 or sd ≤ 0.
· The equation for the lognormal cumulative distribution function is:
LOGNORMDIST
Lets see an example in (Column1 Row 1,Column2Row1, Column3Row1)
LOGNORMDIST (n, m,sd)
LOGNORMDIST (C1R1, C2R1,C3R1)
i.e. =LOGNORMDIST (5, 4.5, 2.2) is 0.09472
Syntax
Remarks
Examples
Description
| Column1 | Column2 | Column3 | Column4 | |||
| Row1 | 5 | 4.5 | 2.2 | |||
| Row2 | 0.094718 | 0 | ||||
| Row3 | ||||||
| Row4 | ||||||
| Row5 | ||||||
| Row6 |
 is the value ,
is the value ,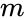 is the mean of
is the mean of 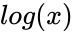 ,
,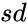 is the standard deviation of
is the standard deviation of