MDETERM(arr)
- where is the array of numeric elements
Description
- This function gives the determinant value of a matrix.
- To calculate the determinant of the matrix we can choose only square matrix.
- i.e., Number rows and number of columns should be equal.Determinant of the identity matrix is always 1. *Determinant of the matrix A is denoted by det(A) or |A|.
- Let A be 2x2 matrix with the elements A=[a b
c d].
- Then det(A)=ad-bc, where a,b,c,d all are real numbers.
- Let A be the 3x3 matrix with the elements A=[a b c
d e f
g h i].
Then |A|=a|e f -b|d f +c|d e
h i| g i| g h|
=a(ei-fh) -b(di-fg)+c(dh-eg)
- Let A be a square matrix of order n. Write A = (a_ij),
- Where aij is the entry on the i number of rows and j number of columns and i=1 to n &j=1 to n.
- For any i and j, set Aij (called the cofactors), then the general formula for determinant of the matrix A , |A|=summation (j=1 to n)a_ij A_ij, for any fixed i.
Also|A|=summation (i=1 to n)a_ij A_ij, for any fixed j.
- This function will give the result as error when
1. Any one of the element in array is empty or contain non-numeric 2. Number of rows is not equal to number of columns
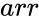 is the array of numeric elements
is the array of numeric elements