CHOLESKY(arr)
- is the array of numeric elements
Description
- This function gives the value of Cholesky factorization.
- It is called Cholesky Decomposition or Cholesky Factorization.
- The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices.
- Every positive definite matrix A can be factored as =
where
is lower triangular with positive diagonal elements is is the conjugate transpose value of
- Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition.
- Here , is set of values to find the factorization value.
Partition matrices in as A= LL^T (Please take the description from http://www.seas.ucla.edu/~vandenbe/103/lectures/chol.pdf )
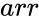 is the array of numeric elements
is the array of numeric elements