Manuals/calci/LEVENESTEST
LEVENESTEST(xRange,ConfidenceLevel,NewTableFlag)
- is the set of values for the test.
- is the value from 0 to 1.
- is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
Description
- This function used to test the Homogeneity of variances.
- Levene's test is used to test the Samples have equal variances.
- Equal variances across samples is called homogeneity of variance or homoscedasticity.
- To do the Levenes test we need the following assumptions:
1.The Samples from the populations are independent of one another. 2. The population under consideration are Normally Distributed.
- For three or more variables the following statistical tests for homogeneity of variances are commonly used:
1.Levene's Test. 2.Bartlett Test.
- Levene's test is an alternative to the Bartlett test.
- If the data surely is of normally distributed or nearly to normally distributed then we can use the Bartlett test.
- The Levene's test is defined as
. =Not all of the variances are equal.
- Normally there are three versions of the Levenes test.
- There are
- 1.Use of Mean.
- 2.Use of Median.
- 3.Use of 10% of Trimmed Mean.
- The Levene test statistic is:
.
- where is the result of the test.
- is the number of different groups to which the sampled cases belong.
- is the total number of cases in all groups.
- is the number of cases in the group.
- case from the group.
- Zij is satisfying the one of the following conditions:
- 1. ,Where is the Mean of the subgroup.
- 2. ,Where is the Median of the subgroup
- 3. ,Where is the 10%Trimmed Mean of the subgroup.
- Levene's Testing Procedure:
- 1. checking the assumptions.
- 2.State the Null(H0) and alternative(H1) hypothesis.
- 3.Decide on the Significance level (α).
- 4.Finding the Critical value and Rejection Region.Here , .
- 5.Compute the Levenes statistic using the formula.
- 6.Then decision of the value of the test statistic,W is falls in the rejection region or if p-value ≤ α, then reject .Otherwise, fail to reject . For the computation p-value we have to use the value of and .
- 7. Finally we have to conclude that the rejection of or fail to rejection according to the test statistic at the significance level.
Example
| X1 | X2 |
| 3067 | 3200 |
| 2730 | 2777 |
| 2840 | 2623 |
| 2913 | 3044 |
| 2789 | 2834 |
- =LEVENESTEST(B1:C5,.05,0)
| Stats | Data1 | Data2 |
|---|---|---|
| Median | 2840 | 2834 |
| Mean | 2867.8 | 2895.6 |
| Variance | 16923.7 | 51713.3 |
| Count | 5 | 5 |
| df | 4 | 4 |
| LevenesTest | Statistics | |
|---|---|---|
| W | 1.0439235110342522 | |
| F-Test | 0.38245649772919 | |
| a | 0.05 | |
| F | 0.32726010523405 | |
| p 1 & 2 Tail | 0.1524069466470822 | 0.3048138932941644 |
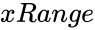 is the set of values for the test.
is the set of values for the test.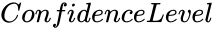 is the value from 0 to 1.
is the value from 0 to 1.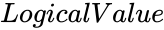 is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.