Manuals/calci/TOEPLITZ
MATRIX("TOEPLITZ",order)
- is the size of the Toeplitz matrix.
Description
- This function gives the matrix of order 3 with the property of toeplitz matrix.
- A Toeplitz matrix is a matrix with the constant values along negative sloping diagonals(descending diagonal from left to right).
- If the i,j element of A is denoted , then we have
.
- Any nxn matrix A of the form:
- The property of Toeplitz matrix is :Toeplitz matrices are persymmetric.
- Symmetric Toeplitz matrices are both centrosymmetric and bisymmetric.
- Toeplitz matrices commute asymptotically.
Examples
- MATRIX("toeplitz",15,1..10)
A =
\begin{bmatrix}
a_{0} & a_{-1} & a_{-2} & \ldots & \ldots &a_{-n+1} \\
a_{1} & a_0 & a_{-1} & \ddots & & \vdots \\
a_{2} & a_{1} & \ddots & \ddots & \ddots& \vdots \\
\vdots & \ddots & \ddots & \ddots & a_{-1} & a_{-2}\\
\vdots & & \ddots & a_{1} & a_{0}& a_{-1} \\
a_{n-1} & \ldots & \ldots & a_{2} & a_{1} & a_{0} \end{bmatrix}
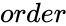 is the size of the Toeplitz matrix.
is the size of the Toeplitz matrix.